Constructing Triangles - JSS2 Mathematics Lesson Note

Constructing a Triangle with a Protractor and a Ruler

Steps:

Draw the Base:

Using a ruler, draw a straight line of the desired length. This will be the base of your triangle.

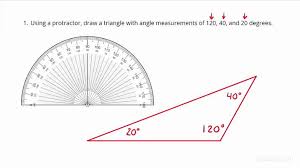
Label the endpoints of the line segment as 𝐴 and 𝐵.


Source:(Studyco.com)

Measure Angles:

Place the protractor at point 𝐴 and measure the desired angle. Mark this point as 𝐶.

Place the protractor at point 𝐵 and measure the desired angle. Mark this point as 𝐷.

Draw the Sides:

Draw a line from 𝐴 to 𝐶 and from 𝐵 to 𝐷.

Intersecting Point:

Extend the lines 𝐴𝐶 and 𝐵𝐷 until they intersect. Label the intersection point as 𝐶.

Example:

Draw a triangle with a base 𝐴𝐵=5 cm, ∠𝐴=60∘, and ∠𝐵=50∘

Steps:

Draw 𝐴𝐵=5.

Place the protractor at 𝐴 and measure 60∘ . Mark the point 𝐶.

Place the protractor at 𝐵 and measure 50∘. Mark the point 𝐷.

Extend the lines 𝐴𝐶 and 𝐵𝐷 until they intersect at 𝐶.

Connect points 𝐴 and 𝐶, and 𝐵 and 𝐶. You have constructed the desired triangle.

Constructing a Right-Angled Triangle

Steps:

Draw the Base:

Draw a line segment 𝐴𝐵 of the desired length. This will be the base.

Construct the Right Angle:

Place the protractor at point 𝐴 and draw a 90∘  angle. Mark a point 𝐶 on this line such that 𝐴𝐶 is the desired length.

Connect the Points:

Draw a line segment from 𝐵 to 𝐶.

Example:

Construct a right-angled triangle with base 𝐴𝐵=6 cm and height 𝐴𝐶=4.

Steps:

Draw 𝐴𝐵=6.

Place the protractor at 𝐴 and draw a 90∘ angle. Measure 𝐴𝐶=4.

Connect points 𝐵 and 𝐶. You have constructed the desired right-angled triangle.