2019 - JAMB Mathematics Past Questions and Answers - page 2
If a fair coin is tossed 3 times, what is the probability of getting at least two heads?
\(\frac{2}{3}\)
\(\frac{4}{5}\)
\(\frac{2}{5}\)
\(\frac{1}{2}\)
The possible outcomes are {HHH, HHT, HTT, HTH, THH, THT, TTH, TTT}
Hence,
P(at least two heads) = \(\frac{4}{8}\)
= \(\frac{1}{2}\)
In how many ways can the word MATHEMATICIAN be arranged?
6794800 ways
2664910 ways
6227020800 ways
129729600 ways
MATHEMATICIAN has 13 letters with 2M, 3A, 2T, 2I.
Hence, the word MATHEMATICIAN can be arranged in \(\frac{13!}{2! 3! 2! 2!}\)
= 129729600 ways
Given matrix M = \(\begin{vmatrix} -2 & 0 & 4 \ 0 & -1 & 6 \ 5 & 6 & 3 \end{vmatrix}\), find \(M^{T} + 2M\)
\(\begin{vmatrix} -4 & 2 & 1\ 6 & 0 & 5 \ 0 & 6 & 2 \end{vmatrix}\)
\(\begin{vmatrix} -6 & 0 & 13\ 0 & -3 & 18 \ 14 & 18 & 9 \end{vmatrix}\)
\(\begin{vmatrix} 5 & 2 & 6 \ 0 & 1 & 1\ 3 & 4 & -7 \end{vmatrix}\)
\(\begin{vmatrix} -4 & 0 & 8 \ 0 & -2 & -16 \ 10 & 12 & 6 \end{vmatrix}\)
Let M represent the matrix.
M = \(\begin{vmatrix} -2 & 0 & 4 \ 0 & -1 & 6 \ 5 & 6 & 3 \end{vmatrix}\)
M\(^{T}\) = \(\begin{vmatrix} -2 & 0 & 5 \ 0 & -1 & 6\ 4 & 6 & 3 \end{vmatrix}\)
2M = \(\begin{vmatrix} -4 & 0 & 8\ 0 & -2 & 12\ 10 & 12 & 6\end{vmatrix}\)
M\(^T\) + 2M = \(\begin{vmatrix} -6 & 0 & 13 \ 0 & -3 & 18 \ 14 & 18 & 9 \end{vmatrix}\)
| Score (x) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Freq (f) | 5 | 7 | 3 | 7 | 11 | 6 | 7 |
Find the mean of the data.
3.26
4.91
6.57
3.0
| Score (x) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| Freq (f) | 5 | 7 | 3 | 7 | 11 | 6 | 7 | 46 |
| fx | 0 | 7 | 6 | 21 | 44 | 30 | 42 | 150 |
Mean (x) = \(\frac{\sum fx}{\sum f}\)
x = \(\frac{150}{46}\)
x = 3.26
| Score (x) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Freq (f) | 5 | 7 | 3 | 7 | 11 | 6 | 7 |
Find the variance
| x | f | fx | (x - \(\bar{x}\)) | (x - \(\bar{x}\))\(^2\) | f(x - \(\bar{x}\))\(^2\) |
| 0 | 5 | 0 | -3.26 | 10.628 | 53.14 |
| 1 | 7 | 7 | -2.26 | 5.108 | 35.756 |
| 2 | 3 | 6 | -1.26 | 1.588 | 4.764 |
| 3 | 7 | 21 | -0.26 | 0.068 | 0.476 |
| 4 | 11 | 44 | 0.74 | 0.548 | 6.028 |
| 5 | 6 | 30 | 1.74 | 3.028 | 18.168 |
| 6 | 7 | 42 | 2.74 | 7.508 | 52.556 |
| 46 | 150 | 170.888 |
Variance = \(\frac{\sum f(x - \bar{x})}{\sum f}\)
= \(\frac{170.888}{46}\)
= 3.72
The locus of a point which moves so that it is equidistant from two intersecting straight lines is the
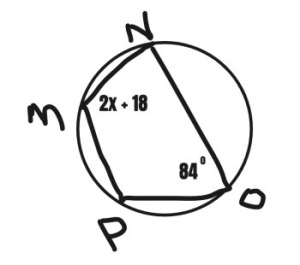
From the cyclic quadrilateral MNOP above, find the value of x.
16°
25°
42°
39°
The sum of two opposite angles of a cyclic quadrilateral is equal to 180°
\(\therefore\) (2x + 18)° + 84° = 180°
2x + 102° = 180° \(\implies\) 2x = 78°
x = 39°
If \(4\sin^2 x - 3 = 0\), find the value of x, when 0° \(\leq\) x \(\leq\) 90°
\(4\sin^2 x - 3 = 0\)
\(4 \sin^2 x = 3 \implies \sin^2 x = \frac{3}{4}\)
\(\sin x = \frac{\sqrt{3}}{2}\)
\(\therefore x = \sin^{-1} (\frac{\sqrt{3}}{2})\)
x = 60°
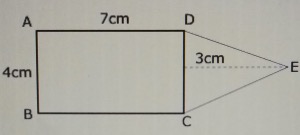
In the figure above, |CD| is the base of the triangle CDE. Find the area of the figure to the nearest whole number.
56 cm\(^2\)
24 cm\(^2\)
42 cm\(^2\)
34 cm\(^2\)
Area of rectangle ABCD = length x breadth
= 7 x 4
= 28 cm\(^2\)
Area of triangle CDE = \(\frac{1}{2}\) base x height
= \(\frac{1}{2} \times 3 \times 4\)
= 6 cm\(^2\)
Hence, area of the figure = 28 cm\(^2\) + 6 cm\(^2\)
= 34 cm\(^2\)
The marks scored by 30 students in a Mathematics test are recorded in the table below:
| Scores (Mark) | 0 | 1 | 2 | 3 | 4 | 5 |
| No of students | 4 | 3 | 7 | 8 | 6 | 2 |
What is the total number of marks scored by the children?
82
15
63
75
| Scores (Mark) | 0 | 1 | 2 | 3 | 4 | 5 | |
| No of students | 4 | 3 | 7 | 8 | 6 | 2 | |
| fx | 0 | 3 | 14 | 24 | 24 | 10 | 75 |
Ans. = 75