2019 - JAMB Mathematics Past Questions and Answers - page 1
Make q the subject of the formula in the equation \(\frac{mn}{a^2} - \frac{pq}{b^2} = 1\)
\(\frac{mn}{a^2} - \frac{pq}{b^2} = 1\)
\(\frac{mn}{a^2} - 1 = \frac{pq}{b^2}\)
\(\frac{mn - a^2}{a^2} = \frac{pq}{b^2}\)
\(pq = \frac{b^2 (mn - a^2)}{a^2}\)
\(q = \frac{b^2(mn - a^2)}{a^2 p}\)
The angle of elevation of the top of a tree from a point on the ground 60m away from the foot of the tree is 78°. Find the height of the tree correct to the nearest whole number.
148m
382m
282m
248m
\(\tan 78 = \frac{h}{60}\)
\(h = 60 \tan 78\)
\(h = 60 \times 4.705 = 282.27m\)
\(\approxeq\) 282m
A binary operation \(\otimes\) is defined by \(m \otimes n = mn + m - n\) on the set of real numbers, for all m, n \(\in\) R. Find the value of 3 \(\otimes\) (2 \(\otimes\) 4).
\(m \otimes n = mn + m - n\)
3 \(\otimes\) (2 \(\otimes\) 4)
2 \(\otimes\) 4 = 2(4) + 2 - 4 = 6
3 \(otimes\) 6 = 3(6) + 3 - 6 = 15
| Age in years | 7 | 8 | 9 | 10 | 11 |
| No of pupils | 4 | 13 | 30 | 44 | 9 |
The table above shows the number of pupils in a class with respect to their ages. If a pie chart is constructed to represent the age, the angle corresponding to 8 years old is
48.6°
56.3°
46.8°
13°
Number of pupils = 4 + 13 + 30 + 44 + 9 = 100
Those of 8 - year olds = 13
On the pie chart, the angle represented by the 8-year olds = \(\frac{13}{100} \times 360°\)
= 46.8°
In a class of 50 students, 40 students offered Physics and 30 offered Biology. How many offered both Physics and Biology?
42
20
70
54
n(Total) = 50
n(Physics) = 40
n(Biology) = 30
Let x = n(Physics and Biology)
Hence,
n(Physics only) = 40 -x
n(Biology only) = 30 - x
40 - x + 30 - x + x = 50
70 - x = 50
x = 20
Rationalize \(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{2} - \sqrt{3}}\)
\(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{2} - \sqrt{3}}\)
= \((\frac{\sqrt{2} + \sqrt{3}}{\sqrt{2} - \sqrt{3}})(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{2} + \sqrt{3}})\)
= \(\frac{2 + \sqrt{6} + \sqrt{6} + 3}{2 - \sqrt{6} + \sqrt{6} - 3}\)
= \(\frac{5 + 2\sqrt{6}}{-1}\)
= \(- 5 - 2\sqrt{6}\)
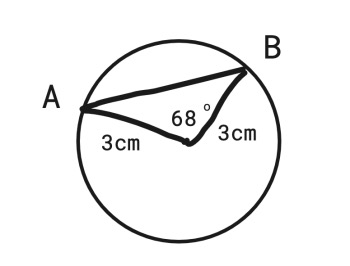
Find the length of the chord |AB| in the diagram shown above.
4.2 cm
4.3 cm
3.2 cm
3.4 cm
Length of chord, l = \(2r \sin (\frac{\theta}{2})\)
= \(2(3) \sin (\frac{68}{2})\)
= \(6 \sin 34\)
= \(6 \times 0.559\)
= 3.354 cm
l = \(\approxeq\) 3.4 cm
Given \(\sin 58° = \cos p°\), find p.
\(\sin \theta = \cos (90 - \theta)\)
\(\sin \theta = \cos (90 - 58)\)
= \(\cos 32\)
\(\frac{\frac{2}{3} \div \frac{4}{5}}{\frac{1}{4} + \frac{3}{5} - \frac{1}{3}}\)
\(\frac{\frac{2}{3} \div \frac{4}{5}}{\frac{1}{4} + \frac{3}{5} - \frac{1}{3}}\)
\(\frac{2}{3} \div \frac{4}{5} = \frac{2}{3} \times \frac{5}{4}\)
= \(\frac{5}{6}\)
\(\frac{1}{4} + \frac{3}{5} - \frac{1}{3} = \frac{15 + 36 - 20}{60}\)
= \(\frac{31}{60}\)
\(\therefore \frac{\frac{2}{3} \div \frac{4}{5}}{\frac{1}{4} + \frac{3}{5} - \frac{1}{3}} = \frac{5}{6} \div \frac{31}{60}\)
= \(\frac{5}{6} \times \frac{60}{31}\)
= \(\frac{50}{31}\)
If \(6x^3 + 2x^2 - 5x + 1\) divides \(x^2 - x - 1\), find the remainder.
9x + 9
A. 2x + 6
B. 6x + 8
C. 5x - 3