Question on: JAMB Mathematics - 1990
A
16\(\pi \sqrt{10}\)cm2
B
20\(\pi \sqrt{10}\)cm2
C
24\(\pi \sqrt{10}\)cm2
D
36\(\pi \sqrt{10}\)cm2
Ask EduPadi AI for a detailed answer
Correct Option: B
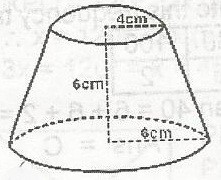
\(\frac{x}{4} = \frac{6 + x}{6}\)
6x = 4(6 + x) = 24 + 4x
x = 12 = c = \(\pi RL - \pi L\)
= \(\pi (6) \sqrt{18^2} + 6^2 - \pi \times 4 \times \sqrt{12^2} + 4^2\)
= 6\(\pi \sqrt{360} - 4 \pi \sqrt{160}\)
= 36\(\pi \sqrt{10} - 16 \pi \sqrt{10}\)
= 20\(\pi \sqrt{10}\)cm2
6x = 4(6 + x) = 24 + 4x
x = 12 = c = \(\pi RL - \pi L\)
= \(\pi (6) \sqrt{18^2} + 6^2 - \pi \times 4 \times \sqrt{12^2} + 4^2\)
= 6\(\pi \sqrt{360} - 4 \pi \sqrt{160}\)
= 36\(\pi \sqrt{10} - 16 \pi \sqrt{10}\)
= 20\(\pi \sqrt{10}\)cm2
Add your answer
Please share this, thanks!
No responses