1998 - JAMB Mathematics Past Questions and Answers - page 3
21
\(\begin{array}{c|c} \text{Average hourly earnings(N)} & 5 - 9 & 10 - 14 & 15 - 19 & 20 - 24\ \hline \text{No. of workers} & 17 & 32 & 25 & 24\end{array}\)
Estimate the mode of the above frequency distribution
Estimate the mode of the above frequency distribution
A
12.2
B
12.27
C
12.9
D
13.4
correct option: b
\(\begin{array}{c|c} \text{Class intervals} & F & \text{Class boundary}\ \hline 5 - 7 & 17 & 4.5 - 9.5\ 10 - 14 & 32 & 9.5 - 14.5\ 15 - 19 & 25 & 14.5 - 19.5\ 20 - 24 & 24 & 19.5 - 24.5 \end{array}\)
mode = 9 + \(\frac{D_1}{D_2 + D_1}\) x C
= 9.5 + \(\frac{5(32 - 17)}{2(32) - 17 - 25}\)
= 9.5 + \(\frac{75}{27}\)
= 12.27
\(\approx\) 2.3
Users' Answers & Commentsmode = 9 + \(\frac{D_1}{D_2 + D_1}\) x C
= 9.5 + \(\frac{5(32 - 17)}{2(32) - 17 - 25}\)
= 9.5 + \(\frac{75}{27}\)
= 12.27
\(\approx\) 2.3
22
Find the variance of the numbers k, k+1, k+2,
A
\(\frac{2}{3}\)
B
1
C
k + 1
D
(k + 1)2
correct option: a
mean (x) = \(\frac{\sum x}{N}\)
= k + k + 1 + k + 3
= \(\frac{3k + 3}{3}\)
= k + 1
\(\begin{array}{c|c} X & (X -X) & (X -X)^2\ \hline k & -1 & 1 \ k + 1 & 0 & 0\ k + 2 & 1 \ \hline & & 2\end{array}\)
Variance (52) = \(\frac{\sum (x - x)^2}{N}\)
= \(\frac{2}{3}\)
Users' Answers & Comments= k + k + 1 + k + 3
= \(\frac{3k + 3}{3}\)
= k + 1
\(\begin{array}{c|c} X & (X -X) & (X -X)^2\ \hline k & -1 & 1 \ k + 1 & 0 & 0\ k + 2 & 1 \ \hline & & 2\end{array}\)
Variance (52) = \(\frac{\sum (x - x)^2}{N}\)
= \(\frac{2}{3}\)
23
Find the positive value of x if the standard deviation of the numbers 1, x + 1 is 6
A
1
B
2
C
3
D
4
correct option: c
mean (x) = \(\frac{1 + x + 1 + 2x + 1}{3}\)
= \(\frac{3x + 3}{3}\)
= 1 + x
\(\begin{array}{c|c} X & (X -X) & (X -X)^2\ \hline 1 & -x & x^2 \ x + 1 & 0 & 0\2x + 1 & x & x^2\ \hline & & 2x^2\end{array}\)
S.D = \(\sqrt{\frac{\sum(x - 7)^2}{\sum f}}\)
= \(\sqrt{(6)}^2\)
= \(\frac{2x^2}{3}\)
= 2x2
= 18
x2 = 9
∴ x = \(\pm\) \(\sqrt{9}\)
= \(\pm\)3
Users' Answers & Comments= \(\frac{3x + 3}{3}\)
= 1 + x
\(\begin{array}{c|c} X & (X -X) & (X -X)^2\ \hline 1 & -x & x^2 \ x + 1 & 0 & 0\2x + 1 & x & x^2\ \hline & & 2x^2\end{array}\)
S.D = \(\sqrt{\frac{\sum(x - 7)^2}{\sum f}}\)
= \(\sqrt{(6)}^2\)
= \(\frac{2x^2}{3}\)
= 2x2
= 18
x2 = 9
∴ x = \(\pm\) \(\sqrt{9}\)
= \(\pm\)3
24
A bag contains 16 red balls and 20 blue balls only. How many white balls must be added to the bag so that the probability of randomly picking a red ball is equal to \(\frac{2}{5}\)
A
4
B
20
C
24
D
40
correct option: a
Number of red balls = 16,
Number of blue balls = 20
Let x represent the No of white balls to be added
∴ Total number of balls = 36 + x
2(36 + x) = 80
= 2x + 80 - 72
= 8
x = \(\frac{8}{2}\)
= 4
Users' Answers & CommentsNumber of blue balls = 20
Let x represent the No of white balls to be added
∴ Total number of balls = 36 + x
2(36 + x) = 80
= 2x + 80 - 72
= 8
x = \(\frac{8}{2}\)
= 4
25
In a recent zonal championship games involving 10 teams, teams X and Y were given probabilities \(\frac{2}{5}\) and \(\frac{1}{3}\) respectively of winning the gold in the football event. What is the probability that either team will win the gold?
A
\(\frac{2}{15}\)
B
\(\frac{7}{15}\)
C
\(\frac{11}{15}\)
D
\(\frac{13}{15}\)
correct option: c
p(x) = \(\frac{2}{5}\) p(y) = \(\frac{1}{3}\)
p(x or y) = p(x ∪ y)
= p(x) + p(y)
= \(\frac{2}{5}\) + \(\frac{1}{3}\)
= \(\frac{11}{5}\)
Users' Answers & Commentsp(x or y) = p(x ∪ y)
= p(x) + p(y)
= \(\frac{2}{5}\) + \(\frac{1}{3}\)
= \(\frac{11}{5}\)
26
If x, y can take values from the set (1, 2, 3, 4), find the probability that the product of x and y is not greater than 6
A
\(\frac{5}{8}\)
B
\(\frac{5}{16}\)
C
\(\frac{1}{2}\)
D
\(\frac{3}{8}\)
correct option: d
\(\begin{vmatrix}& \hline 1 & 2 & 3 & 4\\hline 1 & 1 & 2& 3 & 4\2 & 2& 4 & 6 & 8\ 3& 3& 6& 9 & 12\4 & 4 & 8 & 12& 16\end{vmatrix}\)
p (product of x, and y > 6) = \(\frac{6}{16}\)
= \(\frac{3}{8}\)
Users' Answers & Commentsp (product of x, and y > 6) = \(\frac{6}{16}\)
= \(\frac{3}{8}\)
27
For what value of x does 6 sin (2x - 25)o attain its maximum value in the range 0o \(\leq\) x \(\leq\) 180o
A
12\(\frac{1}{2}\)
B
32\(\frac{1}{2}\)
C
57\(\frac{1}{2}\)
D
147\(\frac{1}{2}\)
correct option: c
y = 6 sin (2x - 25)o
\(\frac{dy}{dx}\) = -12 cos(2x - 25o)
\(\frac{dy}{dx}\) = 0
-12 cos x (2x - 25o) = 0
= cos(2x - 25o) = 0
= 2x - 25o = cos-1(0)
= 2x - 25o
= 90o
x = \(\frac{115}{2}\)
Users' Answers & Comments\(\frac{dy}{dx}\) = -12 cos(2x - 25o)
\(\frac{dy}{dx}\) = 0
-12 cos x (2x - 25o) = 0
= cos(2x - 25o) = 0
= 2x - 25o = cos-1(0)
= 2x - 25o
= 90o
x = \(\frac{115}{2}\)
28
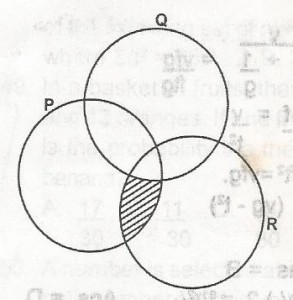
A
(P \(\cap\) Q) \(\cup\) R
B
(P \(\cap\) Q) \(\cap\) R
C
(P \(\cap\) Q1) \(\cap\) R
D
(P \(\cap\) Q1) \(\cup\) R
correct option: c
Users' Answers & Comments29
A
x \(\leq\) 0, y \(\leq\) 0, 2y + 3x \(\leq\) 6
B
x \(\geq\) 0, y \(\geq\) 3, 3x + 2y \(\geq\) 6
C
x \(\geq\) 2, y \(\geq\) 0, 3x + 2y \(\leq\) 6
D
x \(\geq\) 0, y \(\geq\) 0, 3x + 2y \(\geq\) 6
correct option: a
m = \(\frac{y_2 - y_1}{x_2 - x_2} = \frac{3 - 0}{0 - 2} = \frac{-3}{2}\)
= \(\frac{y - y_1}{x- x_1}\)
m = \(\frac{y - 3}{x}\) \(\geq\) \(\frac{-3}{2}\)
2(y - 3) \(\geq\) - 3x = 2y - 6 \(\geq\) - 3x
= 2y + 3x \(\leq\) 6 ; x \(\leq\) 0, y \(\leq\) 0
Users' Answers & Comments= \(\frac{y - y_1}{x- x_1}\)
m = \(\frac{y - 3}{x}\) \(\geq\) \(\frac{-3}{2}\)
2(y - 3) \(\geq\) - 3x = 2y - 6 \(\geq\) - 3x
= 2y + 3x \(\leq\) 6 ; x \(\leq\) 0, y \(\leq\) 0
30
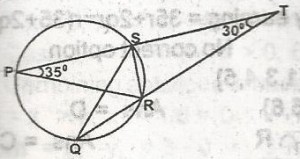
A
20o
B
25o
C
30o
D
35o
correct option: b
< PSR = \(\frac{1}{2}\)(180o) = 90o (angle substended by a semi-circle)
∴ < TSR = 90o
< SRT = 90o - 30o = 60o
< PRS = 90o - 35o = 55o
< PRQ = 180 - (60o + 55o) = 180 - 115o = 65o
< SQR = 35o(angles in the same segment)
< QSR + < SRQ + < SQR = 180o
< QSR + 120o + 35o = 180o
< QSR + 155 = 180o
< QSR = 180o - 155o
= 25o
Users' Answers & Comments∴ < TSR = 90o
< SRT = 90o - 30o = 60o
< PRS = 90o - 35o = 55o
< PRQ = 180 - (60o + 55o) = 180 - 115o = 65o
< SQR = 35o(angles in the same segment)
< QSR + < SRQ + < SQR = 180o
< QSR + 120o + 35o = 180o
< QSR + 155 = 180o
< QSR = 180o - 155o
= 25o