2001 - JAMB Mathematics Past Questions and Answers - page 5
41
Find the range of these fractions:
1/6, 1/3, 3/2, 2/3, 8/9 and 4/3.
1/6, 1/3, 3/2, 2/3, 8/9 and 4/3.
A
3/4
B
5/6
C
7/6
D
4/3
Ask EduPadi AI for a detailed answer
Share this question
42

A
49
B
121
C
25
D
64
Ask EduPadi AI for a detailed answer
Share this question
43

A
7.0
B
8.7
C
9.5
D
11.0
Ask EduPadi AI for a detailed answer
Share this question
44
Team P and Q are involved in a game of football.What is the probability that the game ends in a draw?
A
2/3
B
1/2
C
1/3
D
1/4
Ask EduPadi AI for a detailed answer
Share this question
45
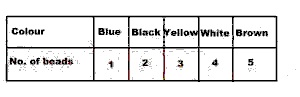
A
7/15
B
2/5
C
1/3
D
1/15
Ask EduPadi AI for a detailed answer
Share this question
46
Find the variance of 2, 6, 8, 6, 2 and 6
A
6
B
5
C
√6
D
√5
Ask EduPadi AI for a detailed answer
Share this question
47
Find the number of ways of selecting 8 subjects from 12 subjects for an examination
A
490
B
495
C
496
D
498
Ask EduPadi AI for a detailed answer
Share this question
48
Find the range of 1/6, 1/3, 3/2, 2/3, 8/9 and 4/3
A
3/4
B
5/6
C
7/6
D
4/3
Ask EduPadi AI for a detailed answer
Share this question
49
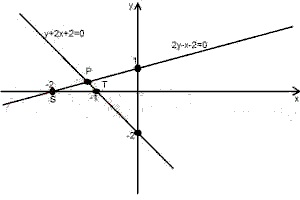
A
2y - x - 2 ≤ 0, y + 2x + 2 ≥ 0, -2 ≤ x ≤ - 1
B
-2 ≤ x ≤ 2, y ≥ 0, y + 2x + 2 ≤ 0, x ≤ 0
C
2y - x - 2 ≤ 0, y + 2x + 2 ≤ 0, y ≥ 0, x ≤ 0
D
2y - x - 2 ≥ 0, y + 2x + 2 ≤ 0, x ≤ 0
Ask EduPadi AI for a detailed answer
Share this question
50
| ⊗ | k | l | m |
| k | l | m | k |
| l | m | k | l |
| m | k | l | m |
The identity element with respect to the multiplication shown in the table above is
A
o
B
m
C
l
D
k
Ask EduPadi AI for a detailed answer
Share this question