EduPadi logo
Home App Pricing Classroom
Blog
👤My Account

Score High in JAMB With EduPadi CBT App

Practice JAMB CBT, get instant results, and understand solutions in-depth with smart AI insights.

Learn more…

2001 - JAMB Mathematics Past Questions and Answers - page 6

51
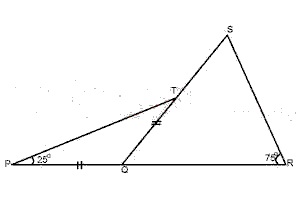
In the figure above, PQR is a straight line segment, PQ = QT. Triangle PQT is an isosceles triangle, ∠SQR is 75o and ∠QPT is 25o. Calculate the value of ∠RST.
A
45o
B
55o
C
25o
D
50o
Ask EduPadi AI for a detailed answer
52
The histogram above shows the distribution of passengers in taxis of a certain motor park. How many taxis have more than 4 passengers
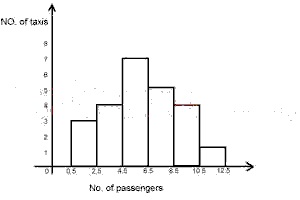
A
16
B
17
C
14
D
15
Ask EduPadi AI for a detailed answer
53
The bar chart above shows different colours of passing a particular point of a certain street in two minutes. What fraction of the total number of cars
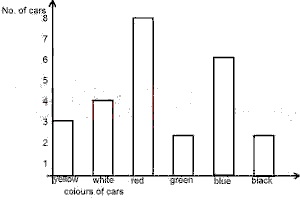
A
3/25
B
2/25
C
1/5
D
4/15
Ask EduPadi AI for a detailed answer
54
Triangle SPT is the solution of the linear inequalities
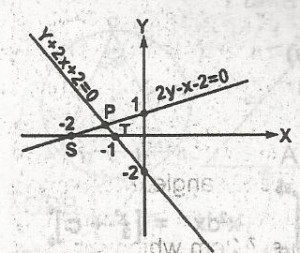
A
2y - x - 2 \(\leq\) 0, y + 2x + 2 \(\geq\) 0, x \(\geq\) 0
B
2y - x - 2 \(\geq\) 0, y + 2x + 2 \(\leq\) 0, -2 \(\geq\) x \(\geq\) -1
C
-2 \(\geq\) x \(\geq\) 2, y \(\leq\) 0, y + 2x + 2 \(\geq\) 0, x \(\geq\) 0
D
2y - x - 2 \(\geq\) 0, y + 2x + 2 \(\geq\) 0, y \(\leq\) 0, x \(\geq\) 0
Ask EduPadi AI for a detailed answer
55
In the figure PQR a straight line segment, PQ = QT. Triangle PQT is an isosceles triangle, < SRQ is 75o and < QPT IS 25o. Calculate the value of < RST
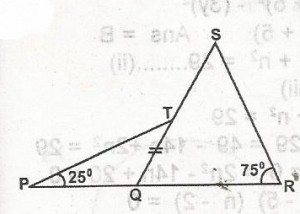
A
50o
B
25o
C
55o
D
45o
Ask EduPadi AI for a detailed answer
56
Find the value of \(\theta\) in the diagram
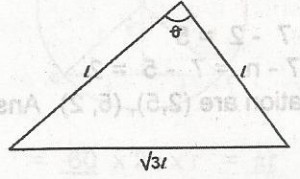
A
60o
B
100o
C
120o
D
30o
Ask EduPadi AI for a detailed answer
57
The bar chart shows different colours of cars passing a particular point of a certain street in two minutes. What fraction of the cars is yellow
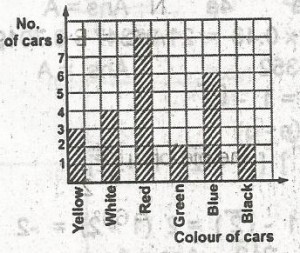
A
\(\frac{1}{5}\)
B
\(\frac{2}{25}\)
C
\(\frac{4}{15}\)
D
\(\frac{3}{25}\)
Ask EduPadi AI for a detailed answer
58
The graph shows the cumulative frequency of the distribution of masses of fertilizer for 48 workers in one institution. Which of the following gives the inter-quartile range?
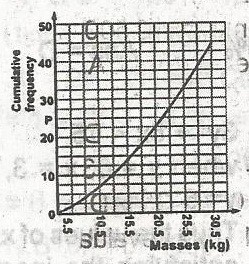
A
\(\frac{1}{2}(Q_3 - Q_1)\)
B
Q3 - Q2
C
Q3 - Q2
D
Q3 - Q1
Ask EduPadi AI for a detailed answer
59
The histogram shows the distribution of passengers in taxis at a certain motor park. How many taxis have more than 4 passengers?
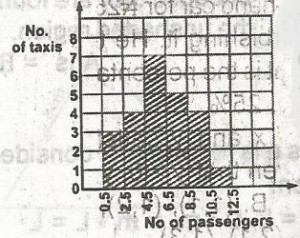
A
17
B
16
C
15
D
14
Ask EduPadi AI for a detailed answer