2004 - JAMB Mathematics Past Questions and Answers - page 1
1
An arc of a circle of length 22 cm subtends an angle of 3xo at the center of the circle. Find the value of x if the diameter of the circle is 14 cm
A
60o
B
120o
C
180o
D
30o
Ask EduPadi AI for a detailed answer
Share this question
2
Find the value of α2 + β2 if α + β = 2 and the distance between points (1, α) and (β, 1)is 3 units
A
14
B
3
C
5
D
11
Ask EduPadi AI for a detailed answer
Share this question
3
The sum of the interior angles of a pentagon is 6x + 6y. Find y in the terms of x
A
y = 90 - x
B
y = 150 - x
C
y = 60 - x
D
y = 120 -x
Ask EduPadi AI for a detailed answer
Share this question
4
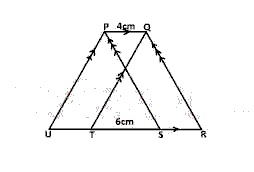
A
60 cm2
B
72 cm2
C
48 cm2
D
24 cm2
Ask EduPadi AI for a detailed answer
Share this question
5
Find the midpoint of the line joining P(-3, 5) and Q(5, -3).
A
(1, 1)
B
(2, 2)
C
(4, 4)
D
(4, -4)
Ask EduPadi AI for a detailed answer
Share this question
6
Determine the locus of a point inside a square PQRS which is eqidistant from PQ and QR
A
The diagonal QS
B
the perpendicular bisector of PQ
C
The diagonal PR
D
side SR
Ask EduPadi AI for a detailed answer
Share this question
7
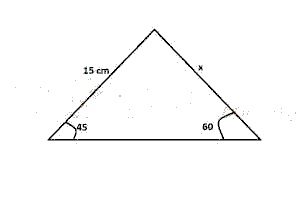
A
15√6
B
20√6
C
3√6
D
5√6
Ask EduPadi AI for a detailed answer
Share this question
8
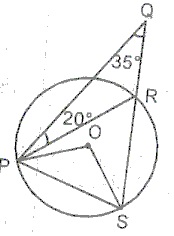
A
45o
B
55o
C
35o
D
40o
Ask EduPadi AI for a detailed answer
Share this question
9
The locus of a point which is 5 cm from the line LM is a
A
line distance 10 cm from LM and parallel to LM
B
pair of line on opposite sides of LM and parallel to it, each distance 5 cm from LM
C
line parallel to LM and 5 cm from LM
D
pair of parallel lines on one side of LM and parallel to LM
Ask EduPadi AI for a detailed answer
Share this question
10
If y = 3 cos(x/3), find dy/dx when x = (3π/2)
A
1
B
-3
C
2
D
-1
Ask EduPadi AI for a detailed answer
Share this question