2007 - JAMB Mathematics Past Questions and Answers - page 5
41
The pie chart above illustrate the amount of private time a student spends in a week studying various subjects. Find the value of k
A
90o
B
60o
C
30o
D
40o
correct option: c
K + 5K + 3K + 75 + 105 = 360 (at a point)
6K + 180 = 360
6K = 360 - 180
6K = 180
k = 180/6 = 30o
Users' Answers & Comments6K + 180 = 360
6K = 360 - 180
6K = 180
k = 180/6 = 30o
42
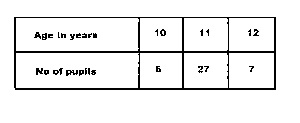
A
27/40
B
17/20
C
3/30
D
33/40
correct option: b
P(At east 11 yrs) = P(11yrs) + P(12yrs)
= 27/40 + 7/40
= 34/40
= 17/20
Users' Answers & Comments= 27/40 + 7/40
= 34/40
= 17/20
43
What is the mean deviation of 3, 5, 8, 11, 12 and 21?
A
4.7
B
60
C
3.7
D
10
correct option: a
Mean \(= \bar{x} = \frac{60}{6} = 10\)
mean deviation \(= \frac{\sum|x-\bar{x}|}{n} = \frac{28}{6}\)
= 4.7
Users' Answers & Commentsmean deviation \(= \frac{\sum|x-\bar{x}|}{n} = \frac{28}{6}\)
= 4.7
44
The table above gives the frequency distribution of marks obtained by a group of students in a test. If the total mark scored is 200, calculate the value of y
A
15
B
13
C
11
D
8
correct option: c
Total mark scored = 200
∴200 = 15 + 4y - 4 + 5y + 54 + 28 + 8
200 = 9y + 101
200 - 101 = 9y
99 = 9y
∴y = 11
Users' Answers & Comments∴200 = 15 + 4y - 4 + 5y + 54 + 28 + 8
200 = 9y + 101
200 - 101 = 9y
99 = 9y
∴y = 11
45
In how many ways can 6 subjects be selected from 10 subjects for an examination
A
218
B
216
C
215
D
210
correct option: d
\(^{10}C_6 = \frac{10!}{(10-6)!6!}=\frac{10!}{4!6!}\\
=\frac{(10\times 9\times 8\times 7 \times 6!)}{4\times 3\times 2\times 1\times 6!}\\
=210\)
Users' Answers & Comments46
Integrate \(\frac{x^2 -\sqrt{x}}{x}\) with respect to x
A
\(\frac{x^2}{2}-2\sqrt{x}+K\)
B
\(\frac{2(x^2 - x)}{3x}+K\)
C
\(\frac{x^2}{2}-\sqrt{x}+K\)
D
\(\frac{(x^2 - x)}{3x}+K\)
correct option: a
\(\int \frac{x^2 -\sqrt{x}}{x} = \int \frac{x^2}{x} - \frac{x^{\frac{1}{2}}}{x}\\
\int x - x^{\frac{-1}{2}}\\
=\left(\frac{1}{2}\right)x^2 - \frac{x^{\frac{1}{2}}}{\frac{1}{2}}+K\\
=\frac{x^2}{2}-2x^{\frac{1}{2}}+K\\
=\frac{x^2}{2}-2\sqrt{x}+K\)
Users' Answers & Comments47
If y = x cos x, find dy/dx
A
sin x - x cos x
B
sin x + x cos x
C
cos x + x sin x
D
cos x - x sin x
correct option: d
y = x cos x
dy/dx = 1. cos x + x (-sin x)
= cos x - x sin x
Users' Answers & Commentsdy/dx = 1. cos x + x (-sin x)
= cos x - x sin x
48
Find the value of x for which the function f(x) = 2x3 - x2 - 4x + 4 has a maximum value
A
2/3
B
1
C
- 2/3
D
- 1
correct option: b
f(x) = 2x3 - x2 - 4x – 4
f’(x) = 6x2 - 2x – 4
As f’(x) = 0
Implies 6x2 - 2x – 4 = 0
3x – x – 2 = 0 (By dividing by 2)
(3x – 2)(x + 1) = 0
3x – 2 = 0 implies x = -2/3
Or x + 1 = 0 implies x = -1
f’(x) = 6x2 - 2x – 4
f’’(x) = 12x – 2
At max point f’’(x) < 0
∴f’’(x) = 12x – 2 at x = -1
= 12(-1) – 2
= -12 – 2 = -14
∴Max at x = 1
Users' Answers & Commentsf’(x) = 6x2 - 2x – 4
As f’(x) = 0
Implies 6x2 - 2x – 4 = 0
3x – x – 2 = 0 (By dividing by 2)
(3x – 2)(x + 1) = 0
3x – 2 = 0 implies x = -2/3
Or x + 1 = 0 implies x = -1
f’(x) = 6x2 - 2x – 4
f’’(x) = 12x – 2
At max point f’’(x) < 0
∴f’’(x) = 12x – 2 at x = -1
= 12(-1) – 2
= -12 – 2 = -14
∴Max at x = 1
49
Determine the value of \(\int_0 ^{\frac{\pi}{2}
}(-2cos x)dx\)
}(-2cos x)dx\)
A
-2
B
-1/2
C
-3
D
-3/2
correct option: a
\(\int_0 ^{\frac{\pi}{2}}(-2cos x)dx = [-2sin x + c]_0 ^{\frac{\pi}{2}}\\
=(-2sin\frac{\pi}{2}+c+2sin0-c)\\
=-2sin90+c+2sin0-c\\
=-2(1)+2(0)\\
=-2\)
Users' Answers & Comments50
A binary operation ⊕ on real numbers is defined by x⊕y = xy + x + y for any two real numbers x and y. The value of (-3/4)⊕6 is
A
3/4
B
-9/2
C
45/4
D
-3/4
correct option: a
x⊕y = xy + x + y
= -3/4 (6) + (-3/4) + 6
= -9/2 - 3/4 + 6
= (-18-3+3+24) / 4
= 3/4
Users' Answers & Comments= -3/4 (6) + (-3/4) + 6
= -9/2 - 3/4 + 6
= (-18-3+3+24) / 4
= 3/4