2025 - JAMB Mathematics Past Questions and Answers - page 1
1
Solve the simultaneous equations \(\frac{x}{2} - \frac{y}{5} = 1\) and \(y - \frac{x}{3} = 8\)
A
x = 10, y = -6
B
x = 10, y = 6
C
x = 6, y = 10
D
x = 10, y = 6
2
Calculate the sum of all elements in the inverse of the matrix \(\begin{bmatrix} 1 & 2 \\ 3 & 5 \end{bmatrix}\)
A
1
B
-1
C
2
D
0.5
3
Given that \(A = \frac{\theta}{360}\pi r^2\), express \(\theta\) in terms of A and r
A
\( \theta = \frac{360}{\pi A} \)
B
\( \theta = \frac{360A}{\pi \theta} \)
C
\( \theta = \frac{360A}{\pi r^2} \)
D
\( \theta = \frac{360 r^2}{\pi A} \)
4
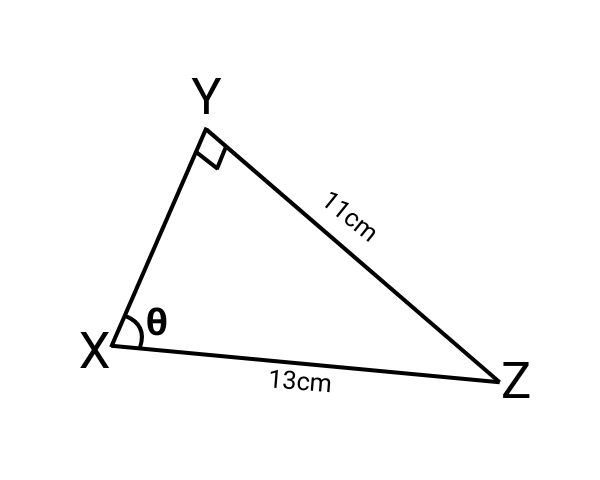
In the triangle XYZ shown, determine Cot \(\theta\) and the length XY respectively
A
\(\frac{\sqrt{48}}{13}\), \(\sqrt{48}\)
B
\(\frac{\sqrt{48}}{11}\), \(\sqrt{48}\)
C
\(\frac{\sqrt{13}}{11}\), \(\sqrt{13}\)
D
\(\frac{13}{\sqrt{48}}\), \(\sqrt{48}\)
5
Determine the probability of obtaining an even number when a fair six-sided die is thrown once.
A
\(\frac{1}{4}\)
B
\(\frac{1}{5}\)
C
\(\frac{1}{2}\)
D
\(\frac{1}{3}\)
6
Given that cos \(\theta\) = \(\frac{x}{y}\), express tan \(\theta\) in terms of x and y
A
\(\frac{\sqrt{y^2 - x^2}}{x}\)
B
\(\frac{\sqrt{y^2 + x^2}}{x}\)
C
\(\frac{\sqrt{y + x}}{x}\)
D
\(\frac{\sqrt{x^2 - y^2}}{x}\)
7
Find the integral of \(y = 4x^3 + 2x + \cos x\)
A
x\(^4\) - x\(^2\) - sin x + C
B
x\(^4\) + x\(^2\) + sin x + C
C
x\(^4\) - x\(^2\) + sin x + C
D
x\(^4\) + x\(^2\) - sin x + C
8
If the probability of survival is p and the probability of death is q, determine the probability that one person survives and the other dies in a two-person accident.
A
p/q
B
pq
C
p - q
D
p + q
9
An amount of #600,000 was obtained after investing a principal y at 5% simple interest for 4 years. Find y.
A
# 570,000
B
# 500,000
C
# 300,000
D
# 400,000
10
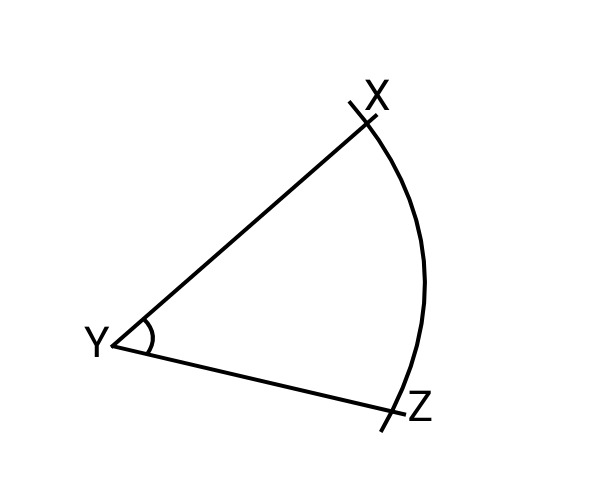
Given the geometric construction shown, determine the value of X\(\hat{Y}\)Z
A
60º
B
30º
C
75º
D
45º
Loading lesson…