1999 - JAMB Mathematics Past Questions and Answers - page 5
41
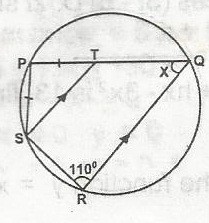
A
70o
B
55o
C
40o
D
35o
Ask EduPadi AI for a detailed answer
Share this question
42
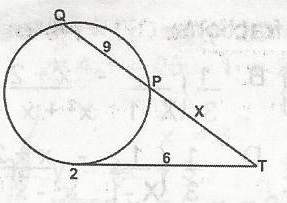
A
3
B
4
C
5
D
6
Ask EduPadi AI for a detailed answer
Share this question
43

A
5cm
B
6cm
C
7cm
D
8cm
Ask EduPadi AI for a detailed answer
Share this question
44
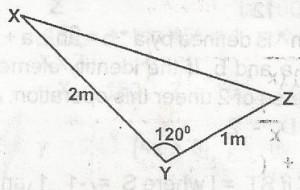
A
\(\sqrt{7m}\)
B
\(\sqrt{6m}\)
C
\(\sqrt{5m}\)
D
\(\sqrt{3m}\)
Ask EduPadi AI for a detailed answer
Share this question
45

A
7
B
8
C
9
D
12
Ask EduPadi AI for a detailed answer
Share this question