1999 - JAMB Mathematics Past Questions and Answers - page 4
31
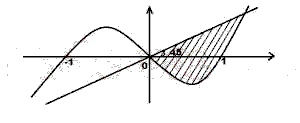
A
y + x - x3 ≥ 0, y - x ≤ 0
B
y - x + x3 ≥ 0, y - x ≤ 0
C
y + x - x3 ≤ 0, y + x ≥ 0
D
y - x + x3 ≤ 0, y + x ≥ 0
correct option: a
y + x - x2 ≥ 0
y = x3 - x
on x axis, y = 0
∴x2 - x = 0
x(x2 - 1) = 0
x = 0 or x2 - 1 = 0
x2 = 1
x = +/-1
∴ x = -1, 0 and 1 which are the roots of the equation y + x - x2 ≥ 0
Also y - x ≤ 0
=> y ≤ 0 + x
∴ the region where y ≤ 0
Users' Answers & Commentsy = x3 - x
on x axis, y = 0
∴x2 - x = 0
x(x2 - 1) = 0
x = 0 or x2 - 1 = 0
x2 = 1
x = +/-1
∴ x = -1, 0 and 1 which are the roots of the equation y + x - x2 ≥ 0
Also y - x ≤ 0
=> y ≤ 0 + x
∴ the region where y ≤ 0
32
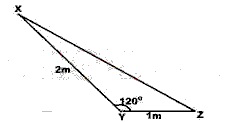
A
√7 m
B
√6 m
C
√5 m
D
√3 m
correct option: a
XY2 = XY2 + Y2 - 2XY.YZ cos 120
XZ2 = 22 + 12 - 2 x 2 1 cos 120
= 4 + 1 -2 x 2 x 1 x -cos(180 - 120)
= 4 + 1 + 4 cos 60
= 5 + 4 x 1/2
= 5 + 2
= 7
XY = √7 m
Users' Answers & CommentsXZ2 = 22 + 12 - 2 x 2 1 cos 120
= 4 + 1 -2 x 2 x 1 x -cos(180 - 120)
= 4 + 1 + 4 cos 60
= 5 + 4 x 1/2
= 5 + 2
= 7
XY = √7 m
33
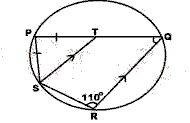
A
70o
B
55o
C
40o
D
35o
correct option: b
PQRS is a cyclic quad
^P = 180 - 110 (opp ∠s of a cyclic quad)
^P = 70
In ΔPTS, ^S = ^T (base ∠s of Isc Δ)
∴^T = (180-70) / 2
= 110/2
= 55o
But ^T x(corr ∠)
∴x =55
Users' Answers & Comments^P = 180 - 110 (opp ∠s of a cyclic quad)
^P = 70
In ΔPTS, ^S = ^T (base ∠s of Isc Δ)
∴^T = (180-70) / 2
= 110/2
= 55o
But ^T x(corr ∠)
∴x =55
34
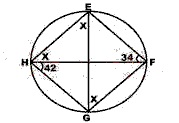
A
34o
B
42o
C
52o
D
76o
correct option: c
∠EFH = ∠EGH(∠s in same segment)
= 34o
∠HEG = ∠HFG(∠s in same segment)
= X
also ∠HFG = ∠EHF (alternate ∠s)
But ∠EHG + ∠EFG =180(opp sof a cyclic quad)
42 + x + 34 + x = 180
2x + 76 = 180
2x = 180 - 76
2x = 104
x = 52o
Users' Answers & Comments= 34o
∠HEG = ∠HFG(∠s in same segment)
= X
also ∠HFG = ∠EHF (alternate ∠s)
But ∠EHG + ∠EFG =180(opp sof a cyclic quad)
42 + x + 34 + x = 180
2x + 76 = 180
2x = 180 - 76
2x = 104
x = 52o
35
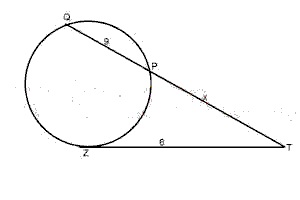
A
3
B
4
C
5
D
6
36
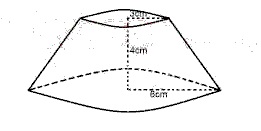
A
5cm
B
6cm
C
7cm
D
8cm
correct option: a
ΔABE and ΔACD are similar
6x = 3(x+4)
6x = 3x + 12
3x = 12
x = 4
In ΔACD; L2 = (4+4)2 + 62
= 82 + 62
= 64 + 36
= 100
L =
√ 100
= 10cm
In ABE, AE2 = 42 + 32
= 16 + 9
= 25
AE = 5cm
∴L = 10 - 5
= 5cm
Users' Answers & Comments| ∴ | x |
| |||
| x+4 |
6x = 3(x+4)
6x = 3x + 12
3x = 12
x = 4
In ΔACD; L2 = (4+4)2 + 62
= 82 + 62
= 64 + 36
= 100
L =
√ 100
= 10cm
In ABE, AE2 = 42 + 32
= 16 + 9
= 25
AE = 5cm
∴L = 10 - 5
= 5cm
37
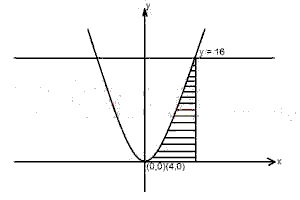
A
64 square units
B
128/3 square units
C
64/3 square units
D
32 square units
correct option: c
\(\int_0 ^4 x^2 dx = \left[\frac{1}{3}x^2+C\right]_0 ^4\\
=\frac{1}{3}\times 4^3 - \frac{1}{3}\times 0^3\\
=\frac{64}{3}-0\\
=\frac{64}{3}\)sq units
Users' Answers & Comments38
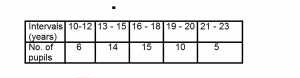
A
35%
B
45%
C
50%
D
60%
correct option: c
% of those above 15 but less than 21 years
age = 25/50 x 100/1
= 50%
Users' Answers & Commentsage = 25/50 x 100/1
= 50%
39
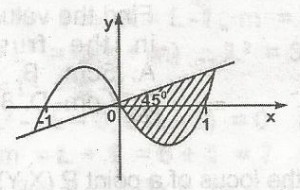
A
y + x - x \(\leq\) 0, y - x \(\leq\) 0
B
y - x + x, 3 \(\leq\) 0, y - x \(\geq\) 0
C
y + x - 3 \(\geq\) 0, y + x \(\leq\) 0
D
y - x + x3 \(\geq\) 0, y + x \(\leq\) 0
correct option: c
Users' Answers & Comments40
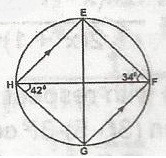
A
34o
B
42o
C
52o
D
76o
correct option: c
< EFH = < EGH = 34o (angles n the same segment)
< GHF = < GEF = 42o(angles in the same segment)
< FOG = 42 + 34 = 76(exterior angle)
< FOG = < EOH = 76(vertically opposite angle)
< EDO = 90o, < DOE = \(\frac{76}{2}\) = 38o
< HEG = 90o - 38o = 52o
Users' Answers & Comments< GHF = < GEF = 42o(angles in the same segment)
< FOG = 42 + 34 = 76(exterior angle)
< FOG = < EOH = 76(vertically opposite angle)
< EDO = 90o, < DOE = \(\frac{76}{2}\) = 38o
< HEG = 90o - 38o = 52o