2003 - JAMB Mathematics Past Questions and Answers - page 2
11
If y = 3 sin(-4x), dy/dx is
A
12x cos (4x)
B
-12x cos (-4x)
C
-12 cos (-4x)
D
12 sin (-4x)
12
Determine the maximum value of y = 3x2 - x3
A
zero
B
2
C
4
D
6
correct option: c
y = 3x2 - x3
dy/dx = 6x - 3x2
as dy/dx = 0
6x - 3x2 = 0
3x (2 - x) = 0
this implies that 2 -x = 0 and 3x = 0
x = 2 (or) 0
But = dy/dx = 6x - 3x2
d2y/dx2 = 6 - 6x at x = 2
= 6 - 6(2)
= -6
y = 3x2 - x3
= 3(2)2 - 23
= 12 - 8
= 4
Users' Answers & Commentsdy/dx = 6x - 3x2
as dy/dx = 0
6x - 3x2 = 0
3x (2 - x) = 0
this implies that 2 -x = 0 and 3x = 0
x = 2 (or) 0
But = dy/dx = 6x - 3x2
d2y/dx2 = 6 - 6x at x = 2
= 6 - 6(2)
= -6
y = 3x2 - x3
= 3(2)2 - 23
= 12 - 8
= 4
13
BY how much is the mean of 30, 56, 31, 55, 43 and 44 less than the median?
A
0.75
B
0.50
C
0.33
D
0.17
correct option: c
\(Mean = \frac{30+56+31+55+43+44}{6}\=\frac{259}{6}=43.167\Median = 30,31,43,44,55,56\=\frac{43+44}{2}=\frac{87}{2}=43.5\Median-mean = 43.3-43.17=0.33\)
Users' Answers & Comments14
The range of 4, 3, 11, 9, 6, 15, 19, 23, 27, 24,21 and 16 is
A
16
B
21
C
23
D
24
15
A
1
B
2
C
3
D
4
correct option: c
\(Mean = \frac{(0 \times 1) + (1 \times 2) + (2 \times 2) + (3 \times 1) + (4 \times 9)}{1 + 2 + 2 + 1 + 9}\=\frac{(0 + 2 + 4 + 3 + 36)}{15}\=\frac{45}{15}=3\)
Users' Answers & Comments16
On the pie chart, there are four sectors of which three angles are 45o, 90o and 135o. If the smallest sector represents N28.00, how much is the largest sector?
A
N96.00
B
N84.00
C
N48.00
D
N42.00
correct option: b
Let the 4th angle be = x
∴ x + 45 + 90 + 135 = 360
x + 270 = 360
x = 360 - 270
x = 90
∴ smallest angle = 45o
45o = N28.00
1o = 28.00/45
135o = (28.00/45) * (135/1)
= N84.00
Users' Answers & Comments∴ x + 45 + 90 + 135 = 360
x + 270 = 360
x = 360 - 270
x = 90
∴ smallest angle = 45o
45o = N28.00
1o = 28.00/45
135o = (28.00/45) * (135/1)
= N84.00
17
If nP3 - 6(nC4) = 0, find the value of n
A
5
B
6
C
7
D
8
correct option: c
\(^{n}P_3 - 6(^{n}C_{4})=0\\frac{n!}{(n-3)!}-6\left( \frac{n!}{(n-4)!4!}\right)=0\\frac{n!}{(n-3)!}=6\left(\frac{n!}{(n-4)!4!}\right)\n!((n-4)!4!)=6n!(n-3)!\((n-4)!4!)=6(n-3)!\\frac{(n-4)!}{(n-3)!}=\frac{6}{4!}\\frac{(n-4)!}{(n-3)(n-4)!}=\frac{6}{4 \times 3\times 2\times 1}\\frac{1}{(n-3)}=]\frac{1}{4}\n-3=4\n=4+3\n=7\)
Users' Answers & Comments18
Find the number of committees of three that can be formed consisting of two men and one woman from four men and three women
A
3
B
6
C
18
D
24
correct option: c
\(^{4}C_2 \times ^{3}C_1 = \left(\frac{4!}{(4-2)!2!}\right)\times\left(\frac{3!}{(3-1)!1!}\right)\=\frac{4!}{2!2!}\times \frac{3!}{2!}\=\frac{4 \times 3 \times 2!}{2 \times 1 \times 2!} \times \frac{3 \times 2!}{2!}\=18\)
Users' Answers & Comments19
A bag contains 5 blacks balls and 3 red balls. Two balls are picked at random without replacement. What is the probability that a black and red balls are picked?
A
15/28
B
13/28
C
5/14
D
3/14
correct option: a
Black balls = 5
Red balls = 3/8
P(B) = 5/8, P(R) = 3/8
P( a Black and a Red) = BR + RB
= (5/8) * (3/7) * (3/8) * (5/7)
= (15/56) + (15/56)
= 30/56
= 15/28
Users' Answers & CommentsRed balls = 3/8
P(B) = 5/8, P(R) = 3/8
P( a Black and a Red) = BR + RB
= (5/8) * (3/7) * (3/8) * (5/7)
= (15/56) + (15/56)
= 30/56
= 15/28
20
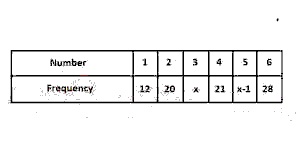
A
19
B
20
C
21
D
22
correct option: b
12 + 20 + x + 21 + x-1 +28 = 120
2x + 80 = 120
2x = 120 - 80
2x = 40
x = 20
Users' Answers & Comments2x + 80 = 120
2x = 120 - 80
2x = 40
x = 20