2003 - JAMB Mathematics Past Questions and Answers - page 3
21
An aeroplane flies due north from airport P to Q and then flies due east R. If Q is equidistant from P and R, find the bearing of P and R
A
90o
B
135o
C
225o
D
270o
Ask EduPadi AI for a detailed answer
Share this question
22
An arc of a circle subtends an angle of 30o on the circumference of a circle of radius 21cm. Find the length of the arc.
A
11cm
B
22cm
C
44cm
D
66cm
Ask EduPadi AI for a detailed answer
Share this question
23
Find the equation of the locus of a point P(x,y) which is equidistant from Q(0,0) and R(2,1).
A
4x + 2y = 5
B
4x - 2y = 5
C
2x + 2y = 5
D
2x + y = 5
Ask EduPadi AI for a detailed answer
Share this question
24
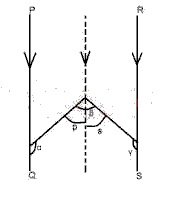
A
360o
B
200o
C
180o
D
90o
Ask EduPadi AI for a detailed answer
Share this question
25
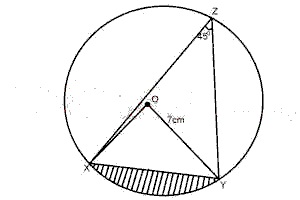
A
84cm2
B
77cm2
C
38cm2
D
14cm2
Ask EduPadi AI for a detailed answer
Share this question
26
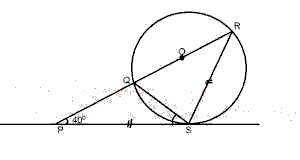
A
40o
B
30o
C
20o
D
10o
Ask EduPadi AI for a detailed answer
Share this question
27
A triangle has vertices P(-1,6), Q(-3, -4) and R(1, -4).Find the midpoint of PQ and QR respectively.
A
(0,-2) and (-1, -4)
B
(-1,0) and (-1,-1)
C
(-2,1) and (0,1)
D
(-2,1) and (-1,-4)
Ask EduPadi AI for a detailed answer
Share this question
28
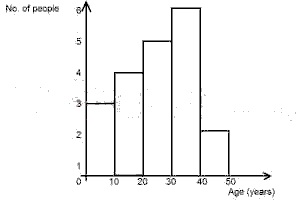
A
15
B
18
C
20
D
21
Ask EduPadi AI for a detailed answer
Share this question
29
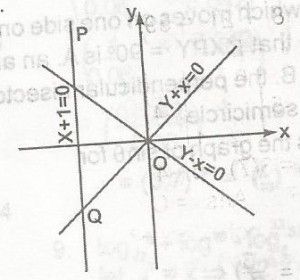
A
x - 1 < 0, y + \(\geq\) 0, y - x \(\geq\) 0
B
x + 1 \(\leq\) 0, y + x \(\geq\) 0, y - x \(\leq\) 0
C
x - 1 \(\geq\) 0, y - x \(\geq\) 0, y + x \(\geq\) 0
D
y + x \(\geq\) 0, y - x \(\leq\) 0
Ask EduPadi AI for a detailed answer
Share this question
30
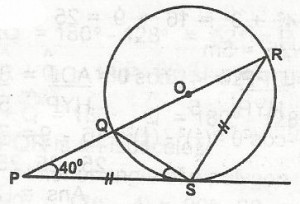
A
20o
B
40o
C
10o
D
30o
Ask EduPadi AI for a detailed answer
Share this question