2008 - JAMB Mathematics Past Questions and Answers - page 3
21
A binary operation on the real set of numbers excluding -1 is such that for all m, n ∈ R, mΔn = m+n+mn. Find the identity element of the operation.
A
1
B
zero
C
-1/2
D
-1
Ask EduPadi AI for a detailed answer
Share this question
22
In the diagram above, PQ//Rs. The size of the angle marked x is
A
100o
B
80o
C
50o
D
30o
Ask EduPadi AI for a detailed answer
Share this question
23
Find the exterior angle of a 12 sided regular polygon
A
12o
B
24o
C
25o
D
30o
Ask EduPadi AI for a detailed answer
Share this question
24
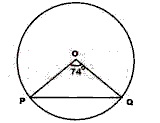
A
90o
B
53o
C
36o
D
26o
Ask EduPadi AI for a detailed answer
Share this question
25
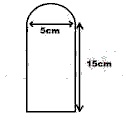
[π = 22/7]
A
12.5 cm2
B
75.0 cm2
C
78.5 cm2
D
84.8 cm2
Ask EduPadi AI for a detailed answer
Share this question
26
Find the angle subtended at the center of a circle by a chord which is equal in length to the radius of the circle.
A
30o
B
45o
C
60o
D
90o
Ask EduPadi AI for a detailed answer
Share this question
27
Find the capacity in liters of a cylindrical well of radius 1 meter and depth 14 meters
[π = 22/7]
[π = 22/7]
A
44,000 liters
B
4,400 liters
C
440 liters
D
44 liters
Ask EduPadi AI for a detailed answer
Share this question
28
The locus of a point equidistant from two points p(6,2) and R(4,2) is a perpendicular bisector of PR passing through
A
(2,5)
B
(5,2)
C
(1,0)
D
(0,1)
Ask EduPadi AI for a detailed answer
Share this question
29
Find the gradient of a line which is perpendicular to the line with the equation 3x + 2y + 1 = 0
A
3/2
B
2/3
C
-2/3
D
-3/2
Ask EduPadi AI for a detailed answer
Share this question
30
If sinθ = 3/5. Find Tanθ
A
3/4
B
3/5
C
2/5
D
1/4
Ask EduPadi AI for a detailed answer
Share this question