2017 - JAMB Mathematics Past Questions and Answers - page 2

3\(^{n + 1}\) × 27\(\frac{n + 1}{81^n}\)

= 3\(^{n + 1}\) × 3 \(\frac{3^{(n + 1)}}{3^{4n}}\)

= 3\(^{n + 1 + 3n + 3 − 4n}\)

= 3\(^{4n − 4n − 1 + 3}\)

= 3²

= 9

The locus of points at a fixed distance from the point P is a circle with the given P at its centre.

The locus of points at a fixed distance from the point Q is a circle with the given point Q at its centre

The locus of points equidistant from two points P and Q i.e line PQ is the perpendicular bisector of the segment determined by the points

Hence, The locus of a point which is equidistant from the line PQ forms a perpendicular line to PQ

Given T = {even numbers from 1 to 12}
= { 2, 4, 6, 8,10, 12}

N = {common factors of 6, 8 and 12}

= {2} Find T n N = {2}

If RST = 60^o

RXT = 2 × RST

(angle at the centre twice angle at the circumference)

RXT = 2 × 60

= 120^o

Range = Highest Number - Lowest Number

Mode is the number with highest occurrence
10, 9, 10, 9, 8, 7, 7, 10, 8, 4, 6,, 9, 10, 9, 7, 10, 6, 5

Range = 10 − 4 = 6

Mode = 10

Sum of range and mode = range + mode = 6 + 10

= 16

Sum to infinity

∑ = arn − 1

= \(\frac{a}{1}\) − r

a = \(\frac{1}{4}\)

r = \(\frac{1}{8}\) ÷ \(\frac{1}{4}\)

r = \(\frac{1}{s}\) × \(\frac{4}{1}\)

= \(\frac{1}{2}\)

S = \(\frac{1 \div 4}{1}\) − \(\frac{1}{2}\)

= \(\frac{1}{4}\) ÷ \(\frac{1}{2}\)

= \(\frac{1}{4}\) × \(\frac{2}{1}\)

= \(\frac{1}{2}\)

2x + x = 180^o

3x = 180^o

x = 60^o (exterior angle of the polygon)

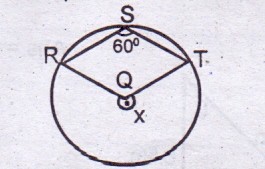
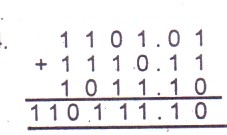
angle = \(\frac{\text{total angle}}{\text{number of sides}}\)

60 = \(\frac{360}{n}\)

n = \(\frac{360}{60}\)

n = 6 sides

Capacity = Volume = 3080m³

base diameter = 14m

radius = \(\frac{\text{diameter}}{2}\)

= 7m

Volume of Cylidner = Capacity of cylinder

πr²h = 3080

\(\frac{22}{7}\) × 7 × 7 × h = 3080

h = \(\frac{3080}{22 \times 7}\)

h = 20m