2020 - JAMB Mathematics Past Questions and Answers - page 3
Calculate the standard deviation of the following data: 7, 8, 9, 10, 11, 12, 13
2
4
12
17
(x - x)\(^2\) = 28
S.D = \(\frac{\sqrt\sum (x - x)^2}{N} = \frac{\sum d^2}{N} = \frac{\sqrt{28}}{7}\)
= \(\sqrt{4}\)
= 2
A number is selected at random between 20 and 30, both numbers inclusive. Find the probability that the number is a prime.
\(\frac{2}{11}\)
\(\frac{5}{11}\)
\(\frac{6}{11}\)
\(\frac{8}{11}\)
Possible outcomes are 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30.
Prime numbers in the possible outcomes: 23, 29.
The probability of choosing a prime number = \(\frac{\text{Number of Prime}}{\text{No. of Total Possible Outcome}}\)
= \(\frac{2}{11}\)
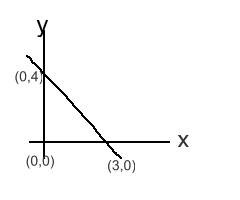
The equation of the line in the graph is
3y = 3x + 12
3y = 3x + 12
3y = -4x + 12
3y = -4x + 9
***
Gradient of line = \(\frac{\text{Change in y}}{\text{Change in x}}\) = \(\frac{y_2 - Y}{x_2 - x}\)
y\(_2\) = 0\(_1\)
Y\(_1\) = 4
x\(_2\) = 3 and x\(_1\) = 0
\(\frac{y_2 - y_1}{x_2 - x_1} = \frac{0 - 4}{3 - 0} = \frac{-4}{3}\)
The general equation of a straight line is y = m x + c , where is the gradient and the coordinates of the y-intercept.
At x = 0, y = c. y-intercept = 4
y = 4x + \(\frac{4}{3}\) multiply through y
3y = 4x + 23
Express the product of 0.0014 and 0.011 in standard form
1.54 x 10\(^{-2}\)
1.54 x 10\(^{-3}\)
1.54 x 10\(^{-2}\)
1.54 x 10\(^{-5}\)
A school boy lying on the ground 30m away from the foot of a water tank towel observes that the angle of elevation of the top of the tank is 60\(^o\). Calculate the height of the tank.
60\(\sqrt{3m}\)
30\(\sqrt{3m}\)
20\(\sqrt{3m}\)
10\(\sqrt{3m}\)
Find the simple interest rate percent annum at which N1000 accumulates to N1240 in 3 years.
6%
8%
10%
12%
I = \(\frac{PRT}{100}\) = 1 = 1240 - 1000 = 240
R = \(\frac{240 \times 100}{100 \times 3}\)
= 8%
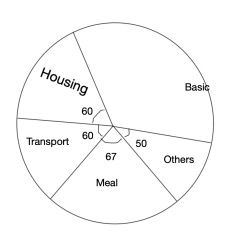
The pie chart shows the income of a civil servant in month. If his monthly income is N6,000. Find his monthly basic salary.
N2,050
N2600
N3,100
N3,450
The total angle in a pie chart = 360\(^o\).
Hence,
360\(^o\) - (60\(^o\) + 60\(^o\) + 67 + 50 = 237\(^o\))
360\(^o\) - 237 = 130\(^o\)
Salary = \(\frac{123}{360} X \frac{N6000}{1}\)
= N2,050
If x is positive real number, find the range of values for which \(\frac{1}{3}\)x + \(\frac{1}{2}\) > \(\frac{1}{4}\)x
x > -\(\frac{1}{6}\)
x > 0
0 < x < 6
0 < x <\(\frac{1}{6}\)
\(\frac{1}{3x}\) + \(\frac{1}{2}\)x
=> \(\frac{2 + 3x}{6x}\) > \(\frac{1}{4x}\)
= 4(2 + 3x) > 6x = 12x\(^2\) - 2x = 0
= 2x(6x - 1) > 0 = x(6x - 1) > 0
(-, -) = x < 0, 6x - 1 > 0. - - - - - - - 1
= x < 0, x < \(\frac{1}{6}\) (solution)
(+, +) = x > 0, 6x - 1 > 0 = x > 0 - - - - -- - - - 2
x > \(\frac{1}{6}\)
Combining (1) and (2):
= x > 0, x < \(\frac{1}{6}\)
= 0 < x < \(\frac{1}{6}\)
Find the value of x if \(\frac{\sqrt{2}}{x + \sqrt{2}}\) = \(\frac{1}{x - \sqrt{2}}\)
3\(\sqrt{2}\) + 4
3\(\sqrt{2}\) - 4
3 - 2\(\sqrt{2}\)
4 + 2\(\sqrt{2}\)
\(\frac{\sqrt{2}}{x + 2}\) = x - \(\frac{1}{\sqrt{2}}\)
x\(\sqrt{2}\) (x - \(\sqrt{2}\)) = x + \(\sqrt{2}\)
x\(\sqrt{2}\) - 2 = x + \(\sqrt{2}\)
= x\(\sqrt{2}\) - x
= 2 + \(\sqrt{2}\)
x (\(\sqrt{2}\) - 1) = 2 + \(\sqrt{2}\)
= \(\frac{2 + \sqrt{2}}{\sqrt{2} - 1} \times \frac{\sqrt{2} + 1}{\sqrt{2} + 1}\)
x = \(\frac{2 \sqrt{2} + 2 + 2 + \sqrt{2}}{2 - 1}\)
= 3\(\sqrt{2}\) + 4
A binary operation x is defined by a x b = a\(^b\). If a x 2 = 2 - a, find the possible values of a?
1, -2
2, -1
2, -2
1, -1
a = b = a\(^2\)
a + 2 = a\(^2\) - - - - - - - 1
a + 2 = 2 - a - - - - - - - - 2
Combining 1 & 2:
a\(^2\) = 2 - a
a\(^2\)+ a - 2 = a\(^2\) + a - 2 = 0
= (a + 2)(a - 1) = 0
a = 1 or - 2