2004 - JAMB Mathematics Past Questions and Answers - page 4
31
Factorize completely ac - 2bc - a + 4b2
A
(a - 2b)(c - a - 2b)
B
(a - 2b)(c + a +2b)
C
(a - 2b)(c - a + 2b)
D
(a - 2b)(c + a - 2b)
correct option: a
ac - 2bc - a2 + 4b2
ac - 2bc - (a2 - 4b2)
ac - 2bc - (a2 -(2b)2)
c(a - 2b) - {(a - 2b)(a + 2b)}
(a - 2b)(c - (a + 2b))
(a - 2b)(c - a - 2b)
Users' Answers & Commentsac - 2bc - (a2 - 4b2)
ac - 2bc - (a2 -(2b)2)
c(a - 2b) - {(a - 2b)(a + 2b)}
(a - 2b)(c - (a + 2b))
(a - 2b)(c - a - 2b)
32
Find the sum to infinity of the series 1/2 , 1/6, 1/18, .....
A
2/3
B
1/3
C
3/4
D
1
correct option: c
\(a=\frac{1}{2}\r=\frac{\frac{1}{6}}{\frac{1}{2}}=\frac{1}{6}\times\frac{2}{1}=\frac{1}{3}\S_n = \frac{a}{1-r}\S_n = \frac{\frac{1}{2}}{1-\frac{1}{3}}\=\frac{\frac{1}{2}}{\frac{3}{2}}\=\frac{1}{2}\times\frac{3}{2}\=\frac{3}{4}\)
Users' Answers & Comments33
The length L of a simple pendulum varies directly as the square of its period T. If a pendulum with period 4 sec. is 64 cm long, find the length of pendulum whose period is 9 sec
A
96 cm
B
324 cm
C
36 cm
D
144 cm
correct option: b
L ∝ T2
L = KT2
K = L/T2 (when T = 4s, L = 64 cm)
K = 64/42
K = 64/16 = 4
∴ ∠ = 4T2
∠ = 4 * 92
= 324 cm
Users' Answers & CommentsL = KT2
K = L/T2 (when T = 4s, L = 64 cm)
K = 64/42
K = 64/16 = 4
∴ ∠ = 4T2
∠ = 4 * 92
= 324 cm
34
Three teachers shared a packet of chalk. The first teacher got 2/5 of the chalk and the second teacher received 2/15 of the remainder. What fraction the the third teacher receive?
A
8/15
B
11/25
C
12/25
D
13/25
correct option: d
First teacher received \(\frac{2}{5}\) ∴Remainder \(= 1 - \frac{2}{5} = \frac{3}{5}\)
2nd teacher received; \(\frac{2}{15} of \frac{3}{5} = \frac{2}{15} \times \frac{3}{5} = \frac{2}{25}\)
3rd teacher will receive; \(1-\frac{2}{5}-\frac{2}{25}=\frac{25-10-2}{15}\=\frac{13}{25}\)
Users' Answers & Comments2nd teacher received; \(\frac{2}{15} of \frac{3}{5} = \frac{2}{15} \times \frac{3}{5} = \frac{2}{25}\)
3rd teacher will receive; \(1-\frac{2}{5}-\frac{2}{25}=\frac{25-10-2}{15}\=\frac{13}{25}\)
35
If 6logx2 - 3logx3 = 3log50.2, find x.
A
8/3
B
4/3
C
3/4
D
3/8
correct option: c
6logx2 - 3logx3 = 3log50.2
= logx26 - 3logx33 = log5(0.2)3
= logx(64/27) = log5(1/5)3
logx(64/27) = log5(1/125)
let logx(64/27) = y
∴xy = 64/27
and log5(1/125) = y
∴ 5y = 1/125
5y = 125-1
5y = 5-3
∴ y = -3
substitute y = -3 in xy = 64/27
implies x-3 = 64/27
1/x3 = 64/27
64x3 = 27
x3 = 27/64
x3 = 3√27/64
x = 3/4
Users' Answers & Comments= logx26 - 3logx33 = log5(0.2)3
= logx(64/27) = log5(1/5)3
logx(64/27) = log5(1/125)
let logx(64/27) = y
∴xy = 64/27
and log5(1/125) = y
∴ 5y = 1/125
5y = 125-1
5y = 5-3
∴ y = -3
substitute y = -3 in xy = 64/27
implies x-3 = 64/27
1/x3 = 64/27
64x3 = 27
x3 = 27/64
x3 = 3√27/64
x = 3/4
36
Find P, if 4516 - P7 = 3056
A
627
B
1167
C
6117
D
1427
correct option: b
4516 - P7 = 3056
P7 = 4516 - 3056
P7 = 1426
convert 1426 = 1 * 62 + 4 * 61 + 2 * 60
= 36 + 24 + 2
= 62
Convert 6210 to base 7
62/7 = 8 R 6
8/7 = 1 R 1
1/7 = 0 R 1
∴P7 = 1167
Users' Answers & CommentsP7 = 4516 - 3056
P7 = 1426
convert 1426 = 1 * 62 + 4 * 61 + 2 * 60
= 36 + 24 + 2
= 62
Convert 6210 to base 7
62/7 = 8 R 6
8/7 = 1 R 1
1/7 = 0 R 1
∴P7 = 1167
37
Given that 3√42x = 16, find the value of x
A
4
B
6
C
3
D
2
correct option: c
3√42x = 16
this implies that (3√42x)3 = (16)3
42x = 42*3
42x = 46
∴ 2x = 6
x = 3
Users' Answers & Commentsthis implies that (3√42x)3 = (16)3
42x = 42*3
42x = 46
∴ 2x = 6
x = 3
38
Evaluate \(\frac{\frac{1}{10}\times\frac{2}{3}+\frac{1}{4}}{\frac{\frac{1}{2}}{\frac{3}{5}}-\frac{1}{4}}\)
A
\(\frac{7}{12}\)
B
\(\frac{19}{35}\)
C
\(\frac{2}{25}\)
D
\(\frac{19}{60}\)
correct option: b
\(\frac{\frac{1}{10}\times\frac{2}{3}+\frac{1}{4}}{\frac{\frac{1}{2}}{\frac{3}{5}}-\frac{1}{4}}\Numerator \hspace{1mm}\frac{1}{10}\times\frac{2}{3}+\frac{1}{4} = \frac{1}{5}+\frac{1}{4}\=\frac{4+15}{60}=\frac{19}{60}\denominator\hspace{1mm}= \frac{\frac{1}{2}}{\frac{3}{5}}-\frac{1}{4}=\frac{1}{2}\times\frac{5}{3}-\frac{1}{4}\=\frac{5}{6}-\frac{1}{4}\=\frac{10-3}{12}\=\frac{7}{12}\\frac{Numerator}{denominator}=\frac{\frac{19}{60}}{\frac{7}{12}}\=\frac{19}{60}\times\frac{12}{7}=\frac{19}{35}\)
Users' Answers & Comments39
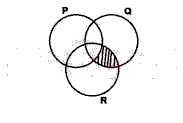
A
Pc ∪ (Q ∩ R)
B
Pc ∩ (Q ∪ R)
C
P ∩ Q
D
Pc ∩ (Q ∩ R)
correct option: d
Users' Answers & Comments40
Simplify \(\frac{1}{\sqrt{3}+2}\) in the form \(a+b\sqrt{3}\)
A
2 -√3
B
-2 - √3
C
2 + √3
D
-2 + √3
correct option: a
\(\frac{1}{\sqrt{3}+2}=\frac{1}{\sqrt{3}+2}\times \frac{\sqrt{3}-2}{\sqrt{3}-2}\=\frac{\sqrt{3}-2}{(\sqrt{3})^{2} -2^{2}}\=\frac{\sqrt{3}-2}{3-4}=\frac{\sqrt{3}-2}{1}\=-\sqrt{3}+2\=2-\sqrt{3}\)
Users' Answers & Comments