2008 - JAMB Mathematics Past Questions and Answers - page 5
41
Find the mean deviation of 2, 4, 5, and 9
A
1
B
2
C
5
D
7
42
In how many ways can the letters of the word ACCEPTANCE be arranged?
A
10! / (2!2!3!)
B
10! / ( 2!3!)
C
10! / (2!2!)
D
10!
correct option: a
ACCEPTANCE = 10 Letters
A = 2 letters
C = 3 letters
E = 2 letters
Can be arranged in 10! / (2!3!2!) ways
Users' Answers & CommentsA = 2 letters
C = 3 letters
E = 2 letters
Can be arranged in 10! / (2!3!2!) ways
43
Find the number of ways of selecting 6 out of 10 subjects for an examination
A
128
B
216
C
215
D
210
correct option: d
\(^{10}C_6 = \frac{10!}{(10-6)!6!}\\
=\frac{10!}{4!6!}\\
=\frac{10\times 9\times 8 \times 7 \times 6!}{4\times 3\times 2\times 1 \times 6!}\\
=210\)
Users' Answers & Comments44
The probability of picking a letter T fr4om the word OBSTRUCTION is
A
1/11
B
2/11
C
3/11
D
4/11
correct option: b
OBSTRUCTION
Total possible outcome = 11
Number of chance of getting T = 2
P(picking T) = 2/11
Users' Answers & CommentsTotal possible outcome = 11
Number of chance of getting T = 2
P(picking T) = 2/11
45
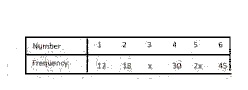
A
3/10
B
1/5
C
1/6
D
1/10
correct option: b
Total possible outcome
12+18+x+30+2x+45 = 105+3x
∴105+3x = 150
3x = 150-105
3x = 45
x = 15
P(obtaining 5) = \(\frac{2x}{(105+3x)}But x= 15\\ =\frac{2(15)}{(105+3(15))}\\ =\frac{30}{(105+45)}\\ =\frac{30}{150}\\ =\frac{1}{5}\)
Users' Answers & Comments12+18+x+30+2x+45 = 105+3x
∴105+3x = 150
3x = 150-105
3x = 45
x = 15
P(obtaining 5) = \(\frac{2x}{(105+3x)}But x= 15\\ =\frac{2(15)}{(105+3(15))}\\ =\frac{30}{(105+45)}\\ =\frac{30}{150}\\ =\frac{1}{5}\)
46
Add 11012, 101112 and 1112
A
1110112
B
1101102
C
1010112
D
1010102
correct option: c
Users' Answers & Comments47
If 125x = 2010, find x
A
2
B
3
C
4
D
5
correct option: b
If 125x = 2010, find x
125x = 1 x 32 + 2 x 31 + 5 x 30
= 1 x 9 + 2 x 3 + 5 x 1
= 9 + 6 + 5
= 20
therefore, 1253 = 2010
x = 3
Users' Answers & Comments125x = 1 x 32 + 2 x 31 + 5 x 30
= 1 x 9 + 2 x 3 + 5 x 1
= 9 + 6 + 5
= 20
therefore, 1253 = 2010
x = 3
48
Evaluate \(\frac{\frac{3}{8} \div \frac {1}{2} - \frac{1}{3}}{\frac{1}{8} \times \frac {2}{3} + \frac{1}{3}}\)
A
\(\frac{1}{4}\)
B
\(\frac{1}{3}\)
C
\(\frac{1}{2}\)
D
1
correct option: d
\(\frac{\frac{3}{8} \div \frac {1}{2} - \frac{1}{3}}{\frac{1}{8} \times \frac {2}{3} + \frac{1}{3}}\)
= \(\frac{\frac{3}{8} \times \frac {2}{1} - \frac{1}{3}}{\frac{1}{8} \times \frac {2}{3} + \frac{1}{3}}\)
= \(\frac{\frac{6}{8} - \frac{1}{3}}{\frac{2}{24} + \frac{1}{3}}\)
= \(\frac{\frac {18 - 8}{24}}{\frac{2 + 8}{24}}\) = \(\frac{\frac{10}{24}}{\frac{10}{24}}\)
= \(\frac{10}{24}\) \(\div\) \(\frac{10}{24}\)
= \(\frac{10}{24}\) x \(\frac{24}{10}\) = 1
Users' Answers & Comments= \(\frac{\frac{3}{8} \times \frac {2}{1} - \frac{1}{3}}{\frac{1}{8} \times \frac {2}{3} + \frac{1}{3}}\)
= \(\frac{\frac{6}{8} - \frac{1}{3}}{\frac{2}{24} + \frac{1}{3}}\)
= \(\frac{\frac {18 - 8}{24}}{\frac{2 + 8}{24}}\) = \(\frac{\frac{10}{24}}{\frac{10}{24}}\)
= \(\frac{10}{24}\) \(\div\) \(\frac{10}{24}\)
= \(\frac{10}{24}\) x \(\frac{24}{10}\) = 1
49
Express 123456 to 3 significant figures
A
123 000
B
124 000
C
125 000
D
126 000
50
Calculate the simple interest on N7500 for 8 years at 5% per annum
A
N3000
B
N600
C
N300
D
N150
correct option: a
Calculate the simple interest on N7500 for 8 years at 5% per annum
S.I = \(\frac{P \times R \times T}{100}\)
S.I = \(\frac{7500 \times 5 \times 8}{100}\)
S.I = \(\frac{300000}{100}\)
S.I = N3000
Users' Answers & CommentsS.I = \(\frac{P \times R \times T}{100}\)
S.I = \(\frac{7500 \times 5 \times 8}{100}\)
S.I = \(\frac{300000}{100}\)
S.I = N3000