2009 - JAMB Mathematics Past Questions and Answers - page 3
21
A binary operation ⊗ defined on the set of integers is such that m⊗n = m + n + mn for all integers m and n. Find the inverse of -5 under this operation, if the identity element is 0
A
-5/4
B
-5/6
C
zero
D
5
correct option: a
m⊗n = m + n + mn
for inverse -5-1 x -5 = e
-5-1 + -5 + (-5-1)(-5) = 0
-5 + (-5-1(-5)) = 5
-5-1.(1 + -5) = 5
-5-1(-4) = 5
-5-1 = -5/4
Users' Answers & Commentsfor inverse -5-1 x -5 = e
-5-1 + -5 + (-5-1)(-5) = 0
-5 + (-5-1(-5)) = 5
-5-1.(1 + -5) = 5
-5-1(-4) = 5
-5-1 = -5/4
22
If Q is\( \left[ \begin{array}{cc}
9 & -2 \\ -7 & 4 \\ \end{array} \right]\) , then |Q| is
9 & -2 \\ -7 & 4 \\ \end{array} \right]\) , then |Q| is
A
-50
B
-22
C
22
D
50
correct option: c
Q = \( \left[ \begin{array}{ccc}
9 & -2 \\ -7 & 4 \\ \end{array} \right]\)
|Q| = 9x4 - (-2x7)
= 36 - 14
= 22
Users' Answers & Comments9 & -2 \\ -7 & 4 \\ \end{array} \right]\)
|Q| = 9x4 - (-2x7)
= 36 - 14
= 22
23
If P \(=\left[\begin{array}{cc}x+3 & x+2\\
x+1 & x-1\end{array}\right]\) evaluate x if |P| = -10
A
-5
B
-2
C
2
D
5
correct option: d
\(P=\left[\begin{array}{cc}x+3 & x+2\\
x+1 & x-1\end{array}\right]\) evaluate x if |P| = -10
(x+3)(x-1) - {(x+1)(x+2)} = -10
x2 - x + 3x - 3 - {x2 + 2x + x + 2} = -10
x2 + 2x - 3 - {x2 + 3x + 2} = -10
-x - 5 = -10
-5 + 10 = x
5 = x
∴x = 5
Users' Answers & Comments(x+3)(x-1) - {(x+1)(x+2)} = -10
x2 - x + 3x - 3 - {x2 + 2x + x + 2} = -10
x2 + 2x - 3 - {x2 + 3x + 2} = -10
-x - 5 = -10
-5 + 10 = x
5 = x
∴x = 5
24
Find the acute angle between the straight lines y = x and y = √3x
A
15o
B
30o
C
45o
D
60o
correct option: a
y = x, Gradient (m1) = 1
y = √3x gradient (m2) = √3
\(tan\theta = \frac{m_2 - m_1}{1+m_2 m_1}\\ tan\theta = \frac{\sqrt{3}-1}{1+\sqrt{3}\times 1}\\ =\frac{1.73 -1 }{1+1.73}=
\frac{0.73}{2.73}=0.268\)
θ = Tan-1 (0.268)
= 15o
Users' Answers & Commentsy = √3x gradient (m2) = √3
\(tan\theta = \frac{m_2 - m_1}{1+m_2 m_1}\\ tan\theta = \frac{\sqrt{3}-1}{1+\sqrt{3}\times 1}\\ =\frac{1.73 -1 }{1+1.73}=
\frac{0.73}{2.73}=0.268\)
θ = Tan-1 (0.268)
= 15o
25
A regular polygon has 150o as the size of each interior angle. How many sides does it have?
A
12
B
10
C
9
D
8
correct option: a
Sum of interior angles of a polygon = each interior ∠ x n
(n-2)180 = 150 x n
180n - 360 = 150n
180n-150n = 360
30n = 360
n = 360/30
n = 12 sides
Users' Answers & Comments(n-2)180 = 150 x n
180n - 360 = 150n
180n-150n = 360
30n = 360
n = 360/30
n = 12 sides
26
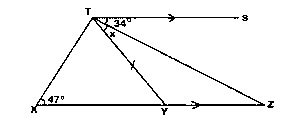
A
47o
B
52o
C
56o
D
99o
correct option: b
In Δ TYX
XY = TY ∴y =47o base ∠s of ISCΔ
But y+x+34+47 = 180 interior
opposite ∠s are supplementary
47 + x + 34 + 47 = 180
x + 128= 180
x = 180- 128
x = 52o
Users' Answers & CommentsXY = TY ∴y =47o base ∠s of ISCΔ
But y+x+34+47 = 180 interior
opposite ∠s are supplementary
47 + x + 34 + 47 = 180
x + 128= 180
x = 180- 128
x = 52o
27
If the hypotenuse of a right angle-triangle isosceles triangle is 2cm. What is the area of the triangle?
A
1/√2 cm2
B
1 cm2
C
√2 cm2
D
2√2 cm2
correct option: b
X2 + x2 = 22
2x2 = 4
x2 = 4/2
x2 = 2
x = +/-√2
Area of Δ = 1/2bh
= 1/2 x √2 x √2
= 2/2
= 1 cm2
Users' Answers & Comments2x2 = 4
x2 = 4/2
x2 = 2
x = +/-√2
Area of Δ = 1/2bh
= 1/2 x √2 x √2
= 2/2
= 1 cm2
28
A chord drawn 5 cm away from the center of a circle of radius 13 cm. Calculate the length of the chord
A
7cm
B
9cm
C
12cm
D
24cm
correct option: d
x2 + 52 = 132
x2 + 25 = 169
x2 = 144
x = √ 144
= 12
Length of the chord AB = 2x
2*12= 24cm
Users' Answers & Commentsx2 + 25 = 169
x2 = 144
x = √ 144
= 12
Length of the chord AB = 2x
2*12= 24cm
29
Find the radius of a sphere whose surface area is 154 cm2
A
7.00 cm
B
3.50 cm
C
3.00 cm
D
1.75 cm
30
Find the locus of a particle which moves in the first quadrant so that it is equidistant from the lines x = 0 and y = 0 (where k is a constant)
A
x + y = 0
B
x - y = 0
C
x + y + k = 0
D
x - y - k = 0
correct option: b
Locus of a particle which moves in the first quadrant so that it is equidistant from the lines
X = 0 and Y = 0 and x = 0 and y = 0 are the x and y axes is the lines bisecting the angle between x and y axes
Users' Answers & CommentsX = 0 and Y = 0 and x = 0 and y = 0 are the x and y axes is the lines bisecting the angle between x and y axes