2016 - JAMB Mathematics Past Questions and Answers - page 5
41
If Q is a factor of 18 and T is prime numbers between 2 and 18. What is Q\(\cap\)T?
A
(2,3)
B
(2,3,18)
C
(2,3,9)
D
(2,3,6)
Ask EduPadi AI for a detailed answer
Share this question
42
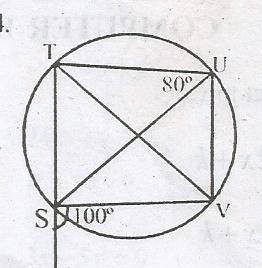
A
60o
B
80o
C
70o
D
50o
Ask EduPadi AI for a detailed answer
Share this question
43
Find the mean of 10, 8, 5, 11, 12, 9, 6, 3, 15, and 23.
A
11.2
B
10
C
10.2
D
11.3
Ask EduPadi AI for a detailed answer
Share this question
44
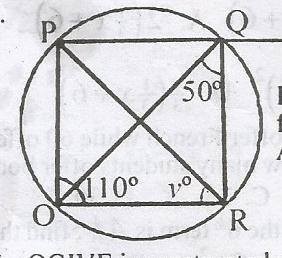
A
70o
B
20o
C
50o
D
30o
Ask EduPadi AI for a detailed answer
Share this question
45
OGIVE is constructed using
A
Third quartile range
B
Semi-quartile range
C
Cummulative frequency table
D
Inter-quartile table
Ask EduPadi AI for a detailed answer
Share this question
46
Rationalize \(\frac{\sqrt{6} - \sqrt{4}}{\sqrt{6} + \sqrt{4}}\)
A
5 + 2 \(\sqrt{6}\)
B
5 - 4 \(\sqrt{6}\)
C
5 + 4 \(\sqrt{6}\)
D
5 - 2 \(\sqrt{6}\)
Ask EduPadi AI for a detailed answer
Share this question
47
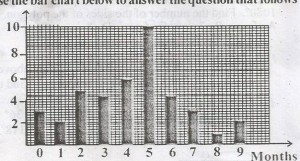
How many students in all took the test?
A
40
B
30
C
10
D
20
Ask EduPadi AI for a detailed answer
Share this question
48
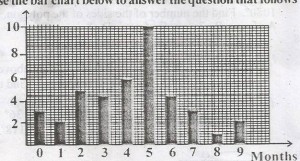
A
4.5
B
4.3
C
4.2
D
4.6
Ask EduPadi AI for a detailed answer
Share this question
49
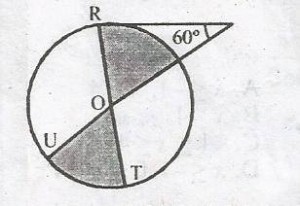
A
\(\frac{1}{3}\)
B
\(\frac{1}{5}\)
C
\(\frac{1}{4}\)
D
\(\frac{1}{6}\)
Ask EduPadi AI for a detailed answer
Share this question
50
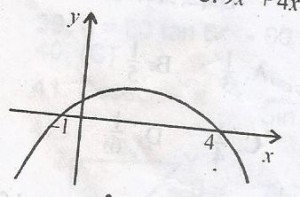
A
x\(\leq\)-1, x \(\geq\)4
B
x\(\leq\)4
C
-1\(\leq\)x\(\leq\)4
D
x\(\leq\)-1, o\(\leq\)x\(\leq\)4
Ask EduPadi AI for a detailed answer
Share this question