1992 - JAMB Mathematics Past Questions and Answers - page 3
21
Q = \(\begin{vmatrix} x & 2 & z \ 3 & y & 2\ 0 & 3 & z \end{vmatrix}\) Where pT is the transpose P calculate /pT/ when x = 0, y = 1 and z = 2
A
48
B
24
C
-24
D
-48
correct option: b
p = \(\begin{vmatrix} 0 & 3 & 0 \ 2 & 1 & 3\ 4 & 2 & 2 \end{vmatrix}\)
PT = \(\begin{vmatrix}0 & 2 & 4 \ 2 & 1 & 3\ 0 & 3 & 2 \end{vmatrix}\)
/pT/ = \(\begin{vmatrix}0 & 2 & 4 \ 3 & 1 & 3\ 0 & 3 & 2 \end{vmatrix}\)
= 0[2 - 6] - 2[6 - 0] + 4[9 - 0]
= 0 - 12 + 36 = 24
Users' Answers & CommentsPT = \(\begin{vmatrix}0 & 2 & 4 \ 2 & 1 & 3\ 0 & 3 & 2 \end{vmatrix}\)
/pT/ = \(\begin{vmatrix}0 & 2 & 4 \ 3 & 1 & 3\ 0 & 3 & 2 \end{vmatrix}\)
= 0[2 - 6] - 2[6 - 0] + 4[9 - 0]
= 0 - 12 + 36 = 24
22
p = \(\begin{vmatrix} x & 3 & 0 \ 2 & y & 3\ 4 & 2 & 4 \end{vmatrix}\)
Q = \(\begin{vmatrix} x & 2 & z \ 3 & y & 2\ 0 & 3 & z \end{vmatrix}\)
PQ is equivalent to
Q = \(\begin{vmatrix} x & 2 & z \ 3 & y & 2\ 0 & 3 & z \end{vmatrix}\)
PQ is equivalent to
A
PPT
B
pp-1
C
qp
D
pp
correct option: a
p = \(\begin{vmatrix} 0 & 3 & 0 \ 2 & 1 & 3\ 4 & 2 & 2 \end{vmatrix}\)
Q = \(\begin{vmatrix} 0 & 2 & 4 \ 3 & 1 & 2\ 0 & 3 & 2 \end{vmatrix}\) = pT
pq = ppT
Users' Answers & CommentsQ = \(\begin{vmatrix} 0 & 2 & 4 \ 3 & 1 & 2\ 0 & 3 & 2 \end{vmatrix}\) = pT
pq = ppT
23
If the angles of quadrilateral are (P + 10)o(2P - 30)o(3P + 20)o and 4po, find p
A
63
B
40
C
36
D
28
correct option: c
Users' Answers & Comments24
Determine the distance on the earth's surface between two town P (latoN, Long 20oN) and Q(Lat 60oN, Long 25oW) (Radius of the earth = 6400km)
A
\(\frac{800\pi}{9}\)km
B
\(\frac{800\sqrt{3\pi}}{9}\)km
C
800\(\pi\) km
D
800\(\sqrt{3\pi}\) km
correct option: b
Users' Answers & Comments25
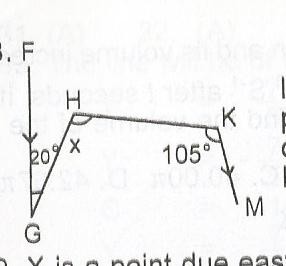
If in the diagram, FG is parallel to KM, find the value of x
A
75o
B
95o
C
105o
D
125o
correct option: b
Users' Answers & Comments26
x is a point due east of point Y on a coast Z is another point on the coast but 63m due south of y. If the distance ZX is 12Km. Calculate the bearing of Z from X
A
240o
B
210o
C
150o
D
60o
correct option: b
Users' Answers & Comments27
The locus of a point which is equidistant from two given fixed points is the
A
perpendicular bisector of the straight line joining them
B
parallel line to the straight line joining them
C
transverse to the straight line joining them
D
angle bisector of 90o which the straight line joining them makes with the horizontal
correct option: a
Users' Answers & Comments28
What is the perpendicular distance of a point (2, 3) from the line 2x - 4y + 3 = 0?
A
\(\frac{\sqrt{5}}{2}\)
B
\(\frac{\sqrt{5}}{20}\)
C
\(\frac{5}{\sqrt{13}}\)
D
6
correct option: a
2x - 4y + 3 = 0
Required distance = \(\frac{(2 \times 2) + 3(-4) + 3}{\sqrt{2^2} + (-4)^2}\)
= \(\frac{4 - 12 + 3}{\sqrt{20}}\)
= \(\frac{-5}{-2\sqrt{5}}\}
= -\{\frac{\sqrt{5}{2}\)
Users' Answers & CommentsRequired distance = \(\frac{(2 \times 2) + 3(-4) + 3}{\sqrt{2^2} + (-4)^2}\)
= \(\frac{4 - 12 + 3}{\sqrt{20}}\)
= \(\frac{-5}{-2\sqrt{5}}\}
= -\{\frac{\sqrt{5}{2}\)
29
find then equation line through (5, 7) parallel to the line 7x + 5y = 12
A
5x + 7y = 120
B
7x + 5y = 70
C
x + y = 7
D
15x + 17y = 90
correct option: b
Equation (5, 7) parallel to the line 7x + 5y = 12
5Y = -7x + 12
y = \(\frac{-7x}{5}\) + \(\frac{12}{5}\)
Gradient = \(\frac{-7}{5}\)
∴ Required equation = \(\frac{y - 7}{x - 5}\) = \(\frac{-7}{5}\) i.e. 5y - 35 = -7x + 35
5y + 7x = 70
Users' Answers & Comments5Y = -7x + 12
y = \(\frac{-7x}{5}\) + \(\frac{12}{5}\)
Gradient = \(\frac{-7}{5}\)
∴ Required equation = \(\frac{y - 7}{x - 5}\) = \(\frac{-7}{5}\) i.e. 5y - 35 = -7x + 35
5y + 7x = 70
30
Given that \(\theta\) is an acute angle and sin \(\theta\) = \(\frac{m}{n}\), find cos \(\theta\)
A
\(\frac{\sqrt{n^2 - m^2}{m}\)
B
\(\frac{\sqrt{(n + m)(n - m)}{n}\)
C
\(\frac{m}{\sqrt{n^2 - m^2}\)
D
\(\sqrt{\frac{n}{n^2 - m^2}}\)
correct option: b
sin \(\theta\) = \(\frac{m}{n}\) x x2
= n2 - m2
x = n2 - m2 cos \(\theta\)
\(\frac{x}{n}\) = \(\frac{n^2 - m^2}{n}\)
cos \(\theta\) = \(\frac{n^2 - m^2}{n}\)
= \(\frac{(n + m)(n - m)}{n}\)
Users' Answers & Comments= n2 - m2
x = n2 - m2 cos \(\theta\)
\(\frac{x}{n}\) = \(\frac{n^2 - m^2}{n}\)
cos \(\theta\) = \(\frac{n^2 - m^2}{n}\)
= \(\frac{(n + m)(n - m)}{n}\)