2013 - JAMB Mathematics Past Questions and Answers - page 4
31
What is the probability that an integer x \((1 \leq x \leq 25)\) chosen at random is divisible by both 2 and 3?
A
\(\frac{1}{25}\)
B
\(\frac{1}{5}\)
C
\(\frac{4}{25}\)
D
\(\frac{3}{4}\)
Ask EduPadi AI for a detailed answer
Share this question
32
A basket contains 9 apples, 8 bananas and 7 oranges. A fruit is picked from the basket, find the probability that it is neither an apple nor an orange.
A
\(\frac{3}{8}\)
B
\(\frac{1}{3}\)
C
\(\frac{7}{24}\)
D
\(\frac{2}{3}\)
Ask EduPadi AI for a detailed answer
Share this question
33
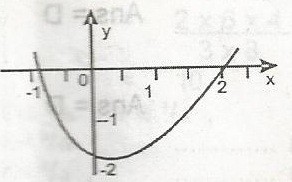
A
y = x2 - x - 2
B
y = x2 - 3x + 2
C
y = x2 - x - 1
D
y = x2 + x - 2
Ask EduPadi AI for a detailed answer
Share this question
34
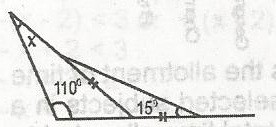
A
30o
B
40o
C
45o
D
15o
Ask EduPadi AI for a detailed answer
Share this question
35

A
110o
B
100o
C
70o
D
130o
Ask EduPadi AI for a detailed answer
Share this question
36
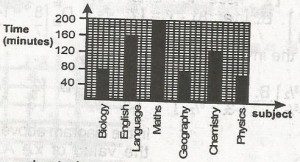
A
460mins
B
720mins
C
960mins
D
200mins
Ask EduPadi AI for a detailed answer
Share this question
37
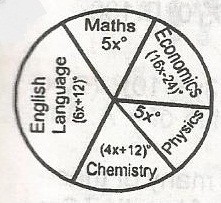
A
30
B
11
C
50
D
20
Ask EduPadi AI for a detailed answer
Share this question