1990 - JAMB Mathematics Past Questions and Answers - page 5
41
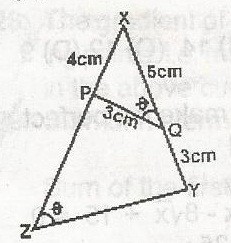
A
8cm
B
6cm
C
4cm
D
3cm
correct option: b
Users' Answers & Comments42
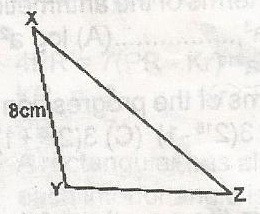
A
16\(\sqrt{2}\)cm
B
8\(\sqrt{2}\)cm
C
4\(\sqrt{2}\)cm
D
22cm
correct option: c
yzx + 105o + 30o = 180o
yzx = 180 - 155 = 45o
(\frac{yz}{sin 30^o} = \frac{8}{sin 45^o})
yz = (\frac{8 \sin 30}{sin 45})
= 8((\frac{1}{2}) = \frac{8}{1} \times \frac{1}{2} \times \frac{\sqrt{2}}{1})
= 4 (\div) (\frac{1}{\sqrt{2}})
= 4(\sqrt{2})cm
Users' Answers & Comments43
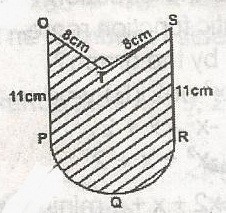
A
125\(\frac{2}{7}\)2
B
149\(\frac{2}{7}\)cm2
C
234\(\frac{1}{7}\)cm2
D
267\(\frac{1}{2}\)cm2
correct option: a
Users' Answers & Comments44
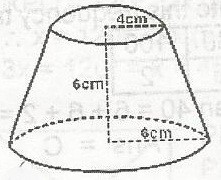
A
16\(\pi \sqrt{10}\)cm2
B
20\(\pi \sqrt{10}\)cm2
C
24\(\pi \sqrt{10}\)cm2
D
36\(\pi \sqrt{10}\)cm2
correct option: b
(\frac{x}{4} = \frac{6 + x}{6})
6x = 4(6 + x) = 24 + 4x
x = 12 = c = (\pi RL - \pi L)
= (\pi (6) \sqrt{18^2} + 6^2 - \pi \times 4 \times \sqrt{12^2} + 4^2)
= 6(\pi \sqrt{360} - 4 \pi \sqrt{160})
= 36(\pi \sqrt{10} - 16 \pi \sqrt{10})
= 20(\pi \sqrt{10})cm2
Users' Answers & Comments