2010 - JAMB Mathematics Past Questions and Answers - page 3
21
\(\begin{array}{c|c} Marks & 2 & 3 & 4 & 5 & 6 & 7 & 8 \ \hline No. of students & 3 & 1 & 5 & 2 & 4 & 2 & 3\end{array}\)
From the table above, if the pass mark is 5, how many students failed the test?
From the table above, if the pass mark is 5, how many students failed the test?
A
6
B
2
C
9
D
7
correct option: c
From the table, the number of students who failed the test is given as:
3 + 1 + 5 = 9
Users' Answers & Comments3 + 1 + 5 = 9
22
\(\begin{array}{c|c} Marks & 1 & 2 & 3 & 4 & 5\ \hline Frequency & 2 & 2 & 8 & 4 & 4\end{array}\)
The table above shows the marks obtained in a given test. How many students took the test?
The table above shows the marks obtained in a given test. How many students took the test?
A
16
B
20
C
13
D
15
correct option: b
from the table, the number of students who took the test is 2 + 2 + 8 + 4 + 4 = 20
Users' Answers & Comments23
\(\begin{array}{c|c} Marks & 1 & 2 & 3 & 4 & 5\ \hline Frequency & 2 & 2 & 8 & 4 & 4\end{array}\)
The table above shows the marks obtained in a given test. Find the mean mark.
The table above shows the marks obtained in a given test. Find the mean mark.
A
3.1
B
3.0
C
3.3
D
3.2
correct option: c
\(\begin{array} & Marks(x) & freq.(f) & fx \1 & 2 & 2 \ 2 & 2 & 4 \ 3 & 8 & 24 \ 4 & 4 & 16\ 5 & 4 & 20 \ \hline & \sum f = 20 & \sum fx = 66\end{array}\)
___________________________________
Mean mark ,\(\bar{x}\) = \(\frac{\sum fx}{\sum f}\)
= \(\frac{66}{20}\)
\(\bar{x}\) = 3.3
Users' Answers & Comments___________________________________
Mean mark ,\(\bar{x}\) = \(\frac{\sum fx}{\sum f}\)
= \(\frac{66}{20}\)
\(\bar{x}\) = 3.3
24
In how many ways can a committee of 2 women and 3 men be chosen from 6 men and 5 women?
A
100
B
200
C
30
D
50
correct option: b
A committee of 2 women and 3 men can be chosen from 6 men and 5 women, in \(^{5}C_{2}\) x \(^{6}C_{3}\) ways
= \(\frac{5!}{(5 - 2)!2!} \times {\frac{6!}{(6 - 3)!3!}}\)
= \(\frac{5!}{3!2!} \times {\frac{6!}{3 \times 3!}}\)
= \(\frac{5 \times 4 \times 3!}{3! \times 2!} \times {\frac{6 \times 5 \times 4 \times 3!}{3! \times 3!}}\)
= \(\frac{5 \times 4}{1 \times 2} \times {\frac{6 \times 5 \times 4}{1 \times 2 \times 3}}\)
= 10 x \(\frac{6 \times 20}{6}\)
= 200
Users' Answers & Comments= \(\frac{5!}{(5 - 2)!2!} \times {\frac{6!}{(6 - 3)!3!}}\)
= \(\frac{5!}{3!2!} \times {\frac{6!}{3 \times 3!}}\)
= \(\frac{5 \times 4 \times 3!}{3! \times 2!} \times {\frac{6 \times 5 \times 4 \times 3!}{3! \times 3!}}\)
= \(\frac{5 \times 4}{1 \times 2} \times {\frac{6 \times 5 \times 4}{1 \times 2 \times 3}}\)
= 10 x \(\frac{6 \times 20}{6}\)
= 200
25
If three unbiased coins are tossed, find the probability that they are all heads
A
\(\frac{1}{2}\)
B
\(\frac{1}{3}\)
C
\(\frac{1}{9}\)
D
\(\frac{1}{8}\)
correct option: d
P(H) = \(\frac{1}{2}\) and P(T) = \(\frac{1}{2}\)
Using the binomial prob. distribution,
(H + T)3 = H3 + 3H2T1 + 3HT2 + T3
Hence the probability that three heads show in a toss of the three coins is H3
= (\(\frac{1}{2}\))3
= \(\frac{1}{8}\)
Users' Answers & CommentsUsing the binomial prob. distribution,
(H + T)3 = H3 + 3H2T1 + 3HT2 + T3
Hence the probability that three heads show in a toss of the three coins is H3
= (\(\frac{1}{2}\))3
= \(\frac{1}{8}\)
26
Find the standard deviation of 2, 3, 5 and 6
A
√6
B
√10
C
√\(\frac{2}{5}\)
D
√\(\frac{5}{2}\)
correct option: d
\(\begin{array}& x & x - \bar{x} & (x - \bar{x})^2 \2 & -2 & 4 \ 3 & -1 & 1 \ 5 & 1 & 1 \ 6 & 2 & 4\ \hline \sum x = 16 & & \sum (x - \bar{x}^2) = 0 \end{array}\)
___________________________________
\(\bar{x}\) = \(\frac{\sum x }{N}\)
= \(\frac{16}{4}\)
= 4
S = \(\sqrt{\frac {(x - \bar{x})^2}{N}}\)
= \(\sqrt{\frac {(10)}{4}}\)
= \(\sqrt{\frac {(5)}{2}}\)
Users' Answers & Comments___________________________________
\(\bar{x}\) = \(\frac{\sum x }{N}\)
= \(\frac{16}{4}\)
= 4
S = \(\sqrt{\frac {(x - \bar{x})^2}{N}}\)
= \(\sqrt{\frac {(10)}{4}}\)
= \(\sqrt{\frac {(5)}{2}}\)
27
A man bought a second-hand photocopying machine for N34000. He serviced i at a cost N2000 and then sold it at a profit of 15%. What was the selling price?
A
N37550
B
N40400
C
N41400
D
42400
correct option: c
Total cost = N34,000 + N2,000
= N36,000
15% = N115
\(\frac{115}{100}\) x N36,000
= N41,400
Users' Answers & Comments= N36,000
15% = N115
\(\frac{115}{100}\) x N36,000
= N41,400
28
W is directly proportional to U. If W = 5 when U = 3, find U when W = \(\frac{2}{7}\)
A
\(\frac{6}{35}\)
B
\(\frac{10}{21}\)
C
\(\frac{21}{10}\)
D
\(\frac{35}{6}\)
correct option: a
W \(\alpha\) U
W = ku
u = \(\frac{w}{k}\); \(\frac{2}{7}\) x \(\frac{3}{5}\)
= \(\frac{6}{35}\)
Users' Answers & CommentsW = ku
u = \(\frac{w}{k}\); \(\frac{2}{7}\) x \(\frac{3}{5}\)
= \(\frac{6}{35}\)
29
Determine the value of x for which (x2 - 1)>0
A
x < -1 or x > 1
B
-1 < x < 1
C
x > 0
D
x < -1
30
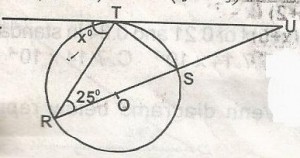
A
75o
B
65o
C
55o
D
50o
correct option: b
In the diagram above, < STU = < TRS = 25o
(< between tangent to circle and a circle and a chord through the point of contact = < in the alternate segment)
< RTS = 90o
(< in a semicircle = 90o)
xo + < RTS + < STU = 180o
xo + 90o + 25o = 180o
xo + 115o = 180o
xo = 180o - 115o = 65o
Users' Answers & Comments(< between tangent to circle and a circle and a chord through the point of contact = < in the alternate segment)
< RTS = 90o
(< in a semicircle = 90o)
xo + < RTS + < STU = 180o
xo + 90o + 25o = 180o
xo + 115o = 180o
xo = 180o - 115o = 65o