2014 - JAMB Mathematics Past Questions and Answers - page 5
41
\(\begin{array}{c|c}
Numbers & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
Frequency & 18 & 22 & 20 & 16 & 10 & 14
\end{array}\)
The table above represents the outcome of throwing a die 100 times. What is the probability of obtaining at least a 4?
Numbers & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
Frequency & 18 & 22 & 20 & 16 & 10 & 14
\end{array}\)
The table above represents the outcome of throwing a die 100 times. What is the probability of obtaining at least a 4?
A
\(\frac{1}{5}\)
B
\(\frac{1}{2}\)
C
\(\frac{2}{5}\)
D
\(\frac{3}{4}\)
correct option: c
Let E demote the event of obtaining at least a 4
Then n(E) = 16 + 10 + 14 = 40
Hence, prob (E) = \(\frac{n(E)}{n(S)}\)
\( = \frac{40}{100}\)
\( = \frac{2}{5}\)
Users' Answers & CommentsThen n(E) = 16 + 10 + 14 = 40
Hence, prob (E) = \(\frac{n(E)}{n(S)}\)
\( = \frac{40}{100}\)
\( = \frac{2}{5}\)
42
A number is chosen at random from 10 to 30 both inclusive. What is the probability that the number is divisible by 3?
A
\(\frac{2}{15}\)
B
\(\frac{1}{10}\)
C
\(\frac{1}{3}\)
D
\(\frac{2}{5}\)
correct option: c
Sample space S = {10, 11, 12, ... 30}
Let E denote the event of choosing a number divisible by 3
Then E = {12, 15, 18, 21, 24, 27, 30} and n(E) = 7
Prob (E) = \(\frac{n(E)}{n(E)}\)
Prob (E) = \(\frac{7}{21}\)
Prob (E) = \(\frac{1}{3}\)
Users' Answers & CommentsLet E denote the event of choosing a number divisible by 3
Then E = {12, 15, 18, 21, 24, 27, 30} and n(E) = 7
Prob (E) = \(\frac{n(E)}{n(E)}\)
Prob (E) = \(\frac{7}{21}\)
Prob (E) = \(\frac{1}{3}\)
43
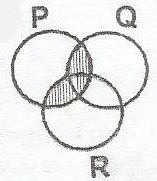
A
(P\(\cap\)Q)\(\cup\)(P\(\cap\)R)
B
(P\(\cup\)Q)\(\cap\)(P\(\cap\)R)
C
(P\(\cup\)Q)\(\cup\)(P\(\cup\)R)
D
(P\(\cap\)Q)\(\cup\)(P\(\cup\)R)
correct option: a
Users' Answers & Comments44
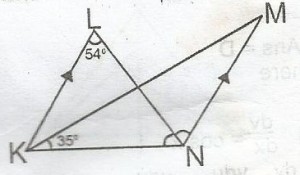
A
91o
B
89o
C
37o
D
19o
correct option: c
In the diagram above, \(\alpha\) = 54o(alternate angles; KL||MN) < KNM = 2\(\alpha\) (LN is bisector of < KNM) = 108o
35o + < KMN + 108o = 180o(sum of angles of \(\bigtriangleup\))
< KMN + 143o = 180o
< KMN = 180o - 143o
= 37o
Users' Answers & Comments35o + < KMN + 108o = 180o(sum of angles of \(\bigtriangleup\))
< KMN + 143o = 180o
< KMN = 180o - 143o
= 37o
45
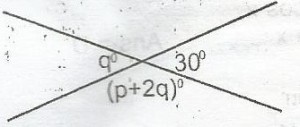
A
135o
B
90o
C
60o
D
45o
correct option: b
In the figure above, qo = 30o (vertically opposite angles)
(P + 2q)o + 30o = 180o(angles on a straight line)
p + 2 x 30o + 30o = 180o
p + 60o + 30o = 180o
p + 90o = 180o
p = 180o - 90o
= 90o
Users' Answers & Comments(P + 2q)o + 30o = 180o(angles on a straight line)
p + 2 x 30o + 30o = 180o
p + 60o + 30o = 180o
p + 90o = 180o
p = 180o - 90o
= 90o
46
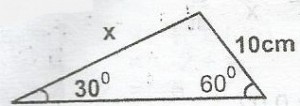
A
20\(\sqrt{3}\)cm
B
10\(\sqrt{3}\)cm
C
5\(\sqrt{3}\)cm
D
4\(\sqrt{3}\)cm
correct option: b
In the figure above, \(\frac{x}{\sin 60^o} = \frac{10}{\sin 30^o}\) (Sine rule)
x = \(\frac{10 \sin 60^o}{\sin 30^o}\)
= 10 x \(\frac{\sqrt{3}}{2} \times \frac{1}{2}\)
= 10 x \(\frac{\sqrt{3}}{2} \times \frac{2}{1}\)
= 10\(\sqrt{3}\)cm
Users' Answers & Commentsx = \(\frac{10 \sin 60^o}{\sin 30^o}\)
= 10 x \(\frac{\sqrt{3}}{2} \times \frac{1}{2}\)
= 10 x \(\frac{\sqrt{3}}{2} \times \frac{2}{1}\)
= 10\(\sqrt{3}\)cm
47
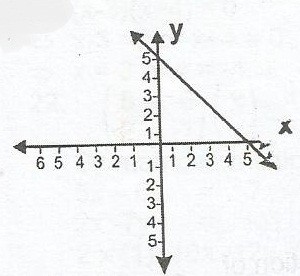
A
y = x + 5
B
y = -x + 5
C
y = x - 5
D
y = -x - 5
correct option: b
(x1, y1) = (0,5)
(x2, y2) = (5, 0)
Using \(\frac{y - y_1}{y_1 - y_1} = \frac{x - x_1}{x_1 - x_1}\)
\(\frac{y - 5}{0 - 5} = \frac{x - 0}{5 - 0}\)
\(\frac{y - 5}{-5} = \frac{x}{5}\)
5(y - 5) = -5x
y - 5 = -x
x + y = 5
y = -x + 5
Users' Answers & Comments(x2, y2) = (5, 0)
Using \(\frac{y - y_1}{y_1 - y_1} = \frac{x - x_1}{x_1 - x_1}\)
\(\frac{y - 5}{0 - 5} = \frac{x - 0}{5 - 0}\)
\(\frac{y - 5}{-5} = \frac{x}{5}\)
5(y - 5) = -5x
y - 5 = -x
x + y = 5
y = -x + 5
48
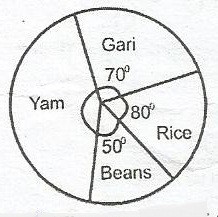
A
N42,000
B
N18,000
C
N16,000
D
N12,000
correct option: c
Angle of sector subtended by yam
= 360o - (70 + 80 + 50)o
= 360o - 200o
= 160o
But \(\frac{80^o}{360^o}\) x T = 8000
T = \(\frac{8000 \times 360^o}{80^o}\)
= N36,000
Hence the amount spent on yam = \(\frac{160^o}{260} \times N36,000\)
= N16,000
Users' Answers & Comments= 360o - (70 + 80 + 50)o
= 360o - 200o
= 160o
But \(\frac{80^o}{360^o}\) x T = 8000
T = \(\frac{8000 \times 360^o}{80^o}\)
= N36,000
Hence the amount spent on yam = \(\frac{160^o}{260} \times N36,000\)
= N16,000